Hàm số mũ
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Hàm số \[y = {a^x}(0 < a \ne 1)\] đồng biến khi nào?
A.a > 1
B.0 < a < 1
C.a ≥ 1
D.a > 0
Chọn khẳng định đúng:
A.Đồ thị hàm số \[y = {a^x}(0 < a \ne 1)\] đi qua điểm (0;0)
B.Đồ thị hàm số \[y = {a^x}(0 < a \ne 1)\]có tiệm cận đứng x=0.
C.Đồ thị hàm số \[y = {a^x}(0 < a \ne 1)\]cắt trục hoành tại duy nhất 1 điểm.
D.Đồ thị hàm số \[y = {a^x}(0 < a \ne 1)\]nằm hoàn toàn phía trên trục hoành.
Chọn mệnh đề đúng:
A.Hàm số \[y = {a^{ - x}}(0 < a \ne 1)\]đồng biến nếu a > 1.
B.Hàm số \[y = {a^{ - x}}(0 < a \ne 1)\]nghịch biến nếu 0 < a < 1.
C.Hàm số \[y = {a^{ - x}}(0 < a \ne 1)\]đồng biến nếu 0 < a < 1.
D.Hàm số \[y = {a^{ - x}}(0 < a \ne 1)\]luôn nghịch biến trên R.
Chọn mệnh đề đúng:
A.Đồ thị hàm số \[y = {2^x}\] trùng với đồ thị hàm số \[y = {\left( {\frac{1}{2}} \right)^{ - x}}\]
B.Đồ thị hàm số \[y = {2^x}\]trùng với đồ thị hàm số \[y = {2^{ - x}}\]
C.Đồ thị hàm số \[y = {2^x}\]đối xứng với đồ thị hàm số \[y = {\left( {\frac{1}{2}} \right)^{ - x}}\] qua trục hoành
D.Đồ thị hàm số \[y = {2^x}\] đối xứng với đồ thị hàm số \[y = {\left( {\frac{1}{2}} \right)^{ - x}}\]qua trục tung.
Chọn mệnh đề đúng:
A.Đồ thị hàm số \[y = {\left( {\frac{1}{3}} \right)^x}\] đối xứng với đồ thị hàm số \[y = - {\left( {\frac{1}{3}} \right)^x}\] qua trục tung.
B.Đồ thị hàm số \[y = {\left( {\frac{1}{3}} \right)^x}\]đối xứng với đồ thị hàm số \[y = - {\left( {\frac{1}{3}} \right)^x}\]qua trục hoành.
C.Đồ thị hàm số \[y = {\left( {\frac{1}{3}} \right)^x}\]đối xứng với đồ thị hàm số \[y = - {\left( {\frac{1}{3}} \right)^x}\]qua đường thẳng y = x
D.Đồ thị hàm số \[y = {\left( {\frac{1}{3}} \right)^x}\]cắt đồ thị hàm số \[y = - {\left( {\frac{1}{3}} \right)^x}\]tại điểm (1;0).
Đồ thị sau là đồ thị hàm số nào?
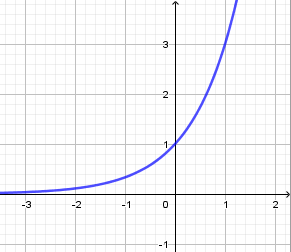
A.\[y = {\left( {\frac{1}{3}} \right)^x}\]
B. \[y = {2^x}\]
C. \[y = 3{x^3}\]
D. \[y = {\left( {\frac{1}{3}} \right)^{ - x}}\]
Đồ thị hàm số dưới đây là của hàm số nào?
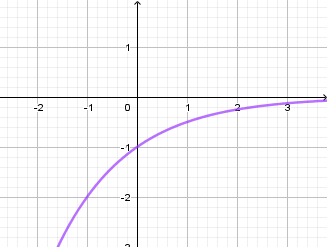
A.\[y = {2^{ - x}}\]
B. \[y = {\left( {\frac{1}{2}} \right)^{ - x}}\]
C. \[y = - {\left( {\frac{1}{2}} \right)^x}\]
D. \[y = - {2^x}\]
Cho các đồ thị hàm số \[y = {a^x},y = {b^x},y = {c^x}(0 < a,b,c \ne 1)\] chọn khẳng định đúng:
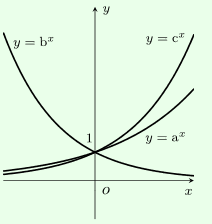
A.c > a > b
B.c > b > a
C.a > c > b
D.b > a > c
Cho hai hàm số \[y = {a^x},y = {b^x}\] với \[1 \ne a,b > 0\;\]lần lượt có đồ thị là (C1),(C2) như hình bên. Mệnh đề nào đúng?
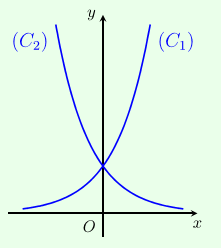
A.0<a<b<1
B.0<b<1<a
C.0<a<1<b
D.0<b<a<1
Hàm số \[y = {2^{\ln x + {x^2}}}\] có đạo hàm là
A.\[\left( {\frac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}\]
B. \[\left( {\frac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2\]
C. \[\frac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\]
D. \[\left( {\frac{1}{x} + 2x} \right)\frac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\]
Cho hàm số \[y = {3^x} + \ln 3\]. Chọn mệnh đề đúng:
A.\[y' = y\ln 3 - {\ln ^2}3\]
B. \[y'.\ln 3 = y + \ln 3\]
C. \[y' = y - {\ln ^2}3\]
D. \[y' = y - \ln 3\]
Cho giới hạn \[I = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{3x}} - {e^{2x}}}}{x}\], chọn mệnh đề đúng:
A.\[{I^2} + 3I = 2\]
B. \[{I^3} + {I^2} - 2 = 0\]
C. \[\frac{{I - 1}}{{I + 1}} = 1\]
D. \[3I - 2 = 2{I^2}\]
Cho a là số thực dương khác 1. Xét hai số thực x1, x2. Phát biểu nào sau đây là đúng?
A.Nếu \[{a^{{x_1}}} < {a^{{x_2}}}\] thì \[{x_1} < {x_2}\]
B.Nếu \[{a^{{x_1}}} < {a^{{x_2}}}\] thì \[{x_1} > {x_2}\]
C.Nếu \[{a^{{x_1}}} < {a^{{x_2}}}\] thì \[\left( {a - 1} \right)\left( {{x_1} - {x_2}} \right) < 0\]
D.Nếu \[{a^{{x_1}}} < {a^{{x_2}}}\] thì \[\left( {a - 1} \right)\left( {{x_1} - {x_2}} \right) > 0\]
Cho hàm số \[f\left( x \right) = {2^x}{.7^{{x^2}}}\]. Khẳng định nào sau đây là khẳng định sai?
A.\[f\left( x \right) < 1 \Leftrightarrow x + {x^2}{\log _2}7 < 0\]
B. \[f\left( x \right) < 1 \Leftrightarrow x\ln 2 + {x^2}\ln 7 < 0\]
C. \[f\left( x \right) < 1 \Leftrightarrow x{\log _7}2 + {x^2} < 0\]
D. \[f\left( x \right) < 1 \Leftrightarrow 1 + x{\log _2}7 < 0\]
Cho các số thực dương a,b khác 1. Biết rằng đường thẳng y=2 cắt đồ thị các hàm số \[y = {a^x};y = {b^x}\;\] và trục tung lần lượt tại A,B,C sao cho C nằm giữa A và B, và AC=2BC. Khẳng định nào dưới đây đúng?
A.\[b = \frac{a}{2}.\]
B. \[b = 2a.\]
C. \[b = {a^{ - 2}}\]
D. \[b = {a^2}\]
Gọi m là GTLN của hàm số \[f(x) = {e^{{x^3} - 3x + 3}}\;\] trên đoạn \[\left[ {0;2} \right]\]Chọn kết luận đúng:
A.\[m = e\]
B. \[m = {e^2}\]
C. \[m = {e^3}\]
D. \[m = {e^5}\]
Gọi m,M lần lượt là GTNN, GTLN của hàm số \[y = {e^{2 - 3x}}\] trên đoạn \[\left[ {0;2} \right].\]Mệnh đề nào sau đây đúng?
A.\[m + M = 1\]
B. \[M - m = e\]
C. \[M.m = \frac{1}{{{e^2}}}\]
D. \[\frac{M}{m} = {e^2}\]
Cho hai số thực dương x,y thỏa mãn \[{2^x} + {2^y} = 4\]. Tìm giá trị lớn nhất PmaxPmax của biểu thức\[P = (2{x^2} + y)(2{y^2} + x) + 9xy\].
A.18
B.12
C.27
D.\[\frac{{27}}{2}\]
Cho hàm số \[f(x) = {(3 - \sqrt 2 )^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}}\]. Xét các khẳng định sau:
Khẳng định 1: \[f(x) > 0 \Leftrightarrow {x^3} + {x^2} > 0\]
Khẳng định 2: \[f(x) > 0 \Leftrightarrow x > - 1\]
Khẳng định 3: \[f(x) < 3 - \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\frac{{3 + \sqrt 2 }}{7}} \right)^{{x^2} + 1}}\]
Khẳng định 4:\[f(x) < 3 + \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} + 1}} < {(3 - \sqrt 2 )^{1 - {x^2}}} + 7\]
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
A.4
B.3
C.1
D.2
Cho hàm số \[f\left( x \right) = \frac{1}{{3 + {2^x}}} + \frac{1}{{3 + {2^{ - x}}}}\]. Trong các khẳng định, có bao nhiêu khẳng định đúng?
1) \[f\prime (x) \ne 0,\forall x \in R\]
2) \[f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2017} \right) = 2017\]
3) \[f({x^2}) = \frac{1}{{3 + {4^x}}} + \frac{1}{{3 + {4^{ - x}}}}\]
A.0
B.1
C.2
D.3
Tìm tập xác định D của hàm số \[y = \sqrt {1 - {3^{{x^2} - 5x + 6}}} \].
A.\[{\rm{D}} = \left[ {2;3} \right]\]
Tính đạo hàm của hàm số \[y = f\left( x \right) = {x^\pi }.{\pi ^x}\] tại điểm x=1.
A.\[f'\left( 1 \right) = \pi .\]
B. \[f'\left( 1 \right) = {\pi ^2} + \ln \pi \]
C. \[f'\left( 1 \right) = {\pi ^2} + \pi \ln \pi .\]
D. \[f'\left( 1 \right) = 1\]
Tập tất cả các giá trị của tham số a để hàm số \[y = {\left( {a - 2} \right)^x}\] nghịch biến trên \(\mathbb{R}\) là:
A.\[\left( {3; + \infty } \right)\]
B. \[\left( { - \infty ;3} \right)\]
C. \[\left( {2;3} \right)\]
D. \[\left( { - \infty ;1} \right)\]
Hàm số nào sau đây nghịch biến trên \[\left( { - \infty ; + \infty } \right)\]?
A.\[y = {\left( {\frac{3}{\pi }} \right)^{ - x}}\]
B. \[y = {\left( {1,5} \right)^x}\]
C. \[y = {\left( {\frac{2}{e}} \right)^x}\]
D. \[y = {\left( {\sqrt 3 + 1} \right)^x}\]
Tính đạo hàm của hàm số \[y = {6^x}\]
A.\[y' = \frac{{{6^x}}}{{\ln 6}}\]
B. \[y' = {6^x}\ln 6\]
C. \[y' = x{.6^{x - 1}}\]
D. \[y' = {6^x}\]
Tập xác định của hàm số \[y = {2^x}\] là:
A.\[.\left[ {0; + \infty } \right)\]
B. \(\mathbb{R}\)
C. \[\left( {0; + \infty } \right)\]
D. \[{\mathbb{R}^ * }\]
Cho hàm số \[y = {e^{2x}} - x\]Chọn khẳng định đúng.
A.Hàm số đồng biến trên khoảng \[\left( { - \ln \sqrt 2 ; + \infty } \right)\]
B.Hàm số đồng biến trên khoảng \[\left( { - \infty ; - \ln 2} \right)\]
C.Hàm số đồng biến trên khoảng \[\left( { - \infty ; - \ln \sqrt 2 } \right)\]
D.Hàm số đồng biến trên khoảng \[\left( { - \ln 2; + \infty } \right)\]
Tìm tất cả các giá trị thực của m để hàm số \[y = {2^{{x^3} - {x^2} + mx + 1}}\] đồng biến trên (1;2)
A.\[m > - 8.\]
B. \[m \ge - 1.\]
C. \[m \le - 8.\]
D. \[m < - 1.\]