Phương trình mũ và một số phương pháp giải
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Phương trình \[{4^{2x + 5}} = {2^{2 - x}}\] có nghiệm là:
A.\[\frac{{ - 8}}{5}\]
B. 3
C. \[\frac{8}{5}\]
D. \[\frac{{12}}{5}\]
Tổng các nghiệm của phương trình \[{3^{{x^4} - 3{x^2}}} = 81\]
A.0
B.1
C.3
D.4
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
A.x=4.
B.x=2.
C.x=5.
D.x=3.
Tìm nghiệm của phương trình \[{9^{\sqrt {x - 1} }} = {e^{\ln 81}}\]
A.x=5
B.x=4
C.x=6
D.x=17
Giải phương trình \[{4^x} = {8^{x - 1}}\]
A.x=−3
B.x=−2
C.x=2
Tìm tập hợp tất cả các nghiệm của phương trình \[{2^{{x^2} + x - 1}} = \frac{1}{2}\].
A.\[\left\{ { - 1;2} \right\}.\]
B. \[\left\{ {0;1} \right\}.\]
C. \[\left\{ { - 1;0} \right\}.\]
D. \[\left\{ { - 2;1} \right\}.\]
Tìm giá trị của a để phương trình \[{(2 + \sqrt 3 )^x} + (1 - a){(2 - \sqrt 3 )^x} - 4 = 0\;\]có 2 nghiệm phân biệt thỏa mãn:\[{x_1} - {x_2} = lo{g_{2 + \sqrt 3 }}3\], ta có a thuộc khoảng:
A.\[(--\infty ;--3)\]
B. \[(--3; + \infty )\]
C. \[(3; + \infty )\]
D. \[(0; + \infty )\]
Tính tổng T tất cả các nghiệm của phương trình\[{4.9^x} - {13.6^x} + {9.4^x} = 0\]
A.T=2.
B.T=3.
C.\[T = \frac{{13}}{4}\]
D. \[T = \frac{1}{4}\]
Tìm tập nghiệm S của phương trình: \[{4^{x + 1}} + {4^{x - 1}} = 272\]
A.\[S = \{ 1\} \]
B. \[S = \{ 3\} \]
C. \[S = \{ 2\} \]
D. \[S = \{ 5\} \]
Giải phương trình \[\sqrt {{3^x} + 6} = {3^x}\]có tập nghiệm bằng:
A.\[\left\{ {1;{{\log }_3}2} \right\}\]
B. \[\left\{ { - 2;3} \right\}\]
C. \[\left\{ 1 \right\}\]
D. \[\left\{ 3 \right\}\]
Tìm tích các nghiệm của phương trình \[{(\sqrt 2 - 1)^x} + {(\sqrt 2 + 1)^x} - 2\sqrt 2 = 0\]
A.2
B.−1
C.0
D.1
Tìm m để phương trình \[{4^x} - \;{2^{x\; + \;3}} + \;3\; = \;m\;\] có đúng 2 nghiệm \[x \in \left( {1;3} \right)\;\].
A.−13<m<−9
B.3<m<9
C.−9<m<3
D. −13<m<3
Tìm tập hợp tất cả các tham số m sao cho phương trình \[{4^{{x^2} - 2x + 1}} - m{.2^{{x^2} - 2x + 2}} + 3m - 2 = 0\;\]có 4 nghiệm phân biệt.
A.\[\left( { - \infty ;1} \right)\]
B. \[\left[ {2; + \infty } \right)\]
C. \[\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\]
D. \[\left( {2; + \infty } \right)\]
Các giá trị thực của tham số m để phương trình : \[{12^x} + (4 - m){.3^x} - m = 0\;\] có nghiệm thuộc khoảng (−1;0) là:
A.\[m \in (\frac{{17}}{{16}};\frac{5}{2})\]
B. \[m \in [2;4]\]
C. \[m \in (\frac{5}{2};6)\]
D. \[m \in (1;\frac{5}{2})\]
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt: \[{9^{1 - x}} + 2(m - 1){3^{1 - x}} + 1 = 0\]
A.m>1
B.m<−1
C.m<0
D.−1<m<0
Tìm giá trị m để phương trình \[{2^{|x - 1| + 1}} + {2^{|x - 1|}} + m = 0\] có nghiệm duy nhất
A.m=3
B.m=18
C.\[m = \frac{1}{8}\]
D.m=1
Cho số thực x thỏa mãn \[2 = {5^{lo{g_3}x}}\;\]. Mệnh đề nào sau đây đúng?
A.\[2 = {3^{{{\log }_5}x}}\]
B. \[5 = {x^{{{\log }_2}3}}\]
C. \[2 = {x^{{{\log }_3}5}}\]
D. \[3 = {5^{\log x}}\]
Biết phương trình \[{9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\]có nghiệm là a. Tính giá trị của biểu thức \[P = a + \frac{1}{2}lo{g_{\frac{9}{2}}}2\;\].
A.\[P = \frac{1}{2}\,\]
B. \[P = 1 - {\log _{\frac{9}{2}}}2\,\]
C. \[P = 1\]
D. \[P = 1 - \frac{1}{2}{\log _{\frac{9}{2}}}2\]
Biết rằng phương trình \[{2^{{x^2} - 1}} = {3^{x + 1}}\]có hai nghiệm là a và b. Khi đó a+b+ab có giá trị bằng
A.\[ - 1 + 2{\log _2}3\]
B. \[1 + {\log _2}3\]
C. -1
D. \[1 + 2{\log _2}3\]
Tìm các giá trị m để phương trình \[{2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3\;}}\]luôn thỏa, \[\forall x \in R\].
A.\[m = \frac{5}{2}\]
B. \[m = \frac{3}{2}\]
C. m=3
D. m=2
Số nghiệm thực phân biệt của phương trình \[{4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0\] là
A.3
B.2
C.0
D.1
Trong các phương trình sau đây, phương trình nào có nghiệm?
A.\[{x^{\frac{2}{3}}} + 5 = 0\]
B. \[{(3x)^{\frac{1}{3}}} + {\left( {x - 4} \right)^{\frac{2}{5}}} = 0\]
C. \[\sqrt {4x - 8} + 2 = 0\]
D. \[2{x^{\frac{1}{2}}} - 3 = 0\]
Số nghiệm thực phân biệt của phương trình \[{2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} = 4\]là:
A.1
B.2
C.3
D.
Phương trình \[x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2}\]có tổng các nghiệm bằng
A.7
B.3
C.5
D.6
Cho aa là số thực dương, khác 1 và thỏa mãn \[\frac{1}{2}({a^\alpha } + {a^{ - \alpha }}) = 1\;\]. Tìm \[\alpha \]
A.\[\alpha = 1\]
B. \[\alpha \in R\]
C. \[\alpha = 0\]
D. \[\alpha = - 1\]
Phương trình \[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\] có tổng các nghiệm gần nhất với số nào dưới đây:
A.0,50
B.0,35
C.0,40
D.0,45
Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất \[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\].
A.0
B.2
C.\( - \frac{1}{2}\)
D. \(\frac{1}{2}\)
Cho hàm số y=f(x) có bảng biến thiên như sau
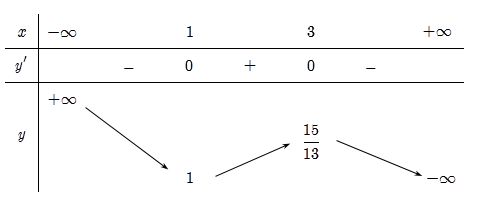
Biết f(0)=76, giá trị lớn nhất của mm để phương trình \[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m\] có nghiệm trên đoạn \[\left[ {0;2} \right]\;\]là
A.\[{e^4}\]
B. \[{e^3}\]
C. \[{e^{\frac{{15}}{{13}}}}\]
D. \[{e^5}\]
Cho các số thực không âm x,y,z thỏa mãn \[{5^x} + {25^y} + {125^z} = 2020\]. Giá trị nhỏ nhất của biếu thức \[T = \frac{x}{6} + \frac{y}{3} + \frac{z}{2}\] là
A.\[\frac{1}{3}{\log _5}2020.\]
B. \[\frac{1}{6}{\log _5}2018.\]
C. \[\frac{1}{6}{\log _5}2020.\]
D. \[\frac{1}{2}{\log _5}2018.\]
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình \[{16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\]có nghiệm dương?
A.1
B.2
C.4
D.3
Cho \[{4^x} + {4^{ - x}} = 7\]. Khi đó biểu thức \[P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}} = \frac{a}{b}\] với \[\frac{a}{b}\] tối giản và \[a,b \in \mathbb{Z}\]. Tích a.b có giá trị bằng
A.10
B.−8
C.8
D.−10
Đề thi THPT QG - 2021 - mã 101
Có bao nhiêu số nguyên y sao cho tồn tại \[x \in (\frac{1}{3};3)\;\] thỏa mãn \[27{\,^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{9x}}\]?
A.27
B.9
C.11
D.12