Sự đồng biến, nghịch biến
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hàm số \[y = f\left( x \right)\;\] đồng biến trên D và \[{x_1},{x_2} \in D\] mà \[{x_1} > {x_2}\], khi đó:
A.\[f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\]
B. \[f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\]
C. \[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\]
D. \[f\left( {{x_2}} \right) \ge f\left( {{x_1}} \right)\]
Cho hàm số y=f(x) nghịch biến và có đạo hàm trên (−5;5). Khi đó:
A.\[f\left( 3 \right) > 0\]
B. \[f'\left( 0 \right) \le 0\]
C. \[f'\left( 0 \right) > 0\]
D. \[f\left( 0 \right) = 0\]
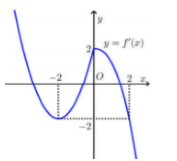
Hình dưới là đồ thị hàm số y=f′(x). Hỏi hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
A.(0;1) và \[\left( {2; + \infty } \right)\]
B.(1;2)
C.\[\left( {2; + \infty } \right)\]
D.(0;1)
Cho hàm số y=f(x) xác định và liên tục trên \(\mathbb{R}\) và có đạo hàm f′(x)=x2−4f′(x)=x2−4. Chọn khẳng định đúng:
A.Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 2} \right)\;\]và \[\left( {2; + \infty } \right)\]
B.Hàm số nghịch biến trên khoảng \[\left( { - 2; + \infty } \right)\]
C.Hàm số đồng biến trên khoảng (−2;2)
D.Hàm số không đổi trên \(\mathbb{R}\)
Cho hàm số y=f(x) xác định và có đạo hàm \[f\prime (x) = 2{x^2}\] trên R. Chọn kết luận đúng:
A.Hàm số đồng biến trên R.
B.Hàm số không xác định tại x=0.
C.Hàm số nghịch biến trên R.
D.Hàm số đồng biến trên \[\left( {0; + \infty } \right)\;\]và nghịch biến trên \[\left( { - \infty ;0} \right)\]
Cho hàm số y=f(x) xác định và có đạo hàm trên (a;b). Chọn kết luận đúng:
A.Nếu \[f\prime (x) \ge 0,\forall x \in (a;b)\;\] thì f(x) đồng biến trên (a;b).
B.Nếu \[f\prime (x) \ge 0,\forall x \in (a;b)\;\]thì f(x) đồng biến trên (a;b).
C.Nếu \[f\prime (x) = 0,\forall x \in (a;b)\;\] thì f(x)=0 trên (a;b).
D.Nếu \[f\prime (x) \le 0,\forall x \in (a;b)\;\] thì f(x) không đổi trên (a;b).
Hàm số \[y = - {x^4} - 2{x^2} + 3\] nghịch biến trên:
A.\[\left( { - \infty ;0} \right)\]
B.\[\left( { - \infty ; - 1} \right)\] và (0;1)
C.R
D.\[\left( {0; + \infty } \right)\]
Cho hàm số y=f(x) có bảng biến thiên như sau:
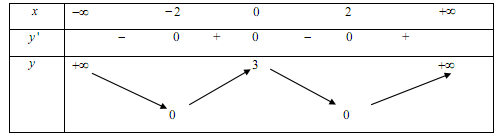
Khẳng định nào sau đây là khẳng định đúng:
A.Hàm số nghịch biến trên \[\left( { - \infty ;2} \right)\]
B.Hàm số nghịch biến trên (−2;0)
C. \[f\left( x \right) \ge 0,\forall x \in R\]
D.Hàm số đồng biến trên (0;3)
Cho hàm số: \[f(x) = - 2{x^3} + 3{x^2} + 12x - 5.\]. Trong các mệnh đề sau, tìm mệnh đề sai?
A.Trên khoảng (−1;1) thì f(x) đồng biến
B.Trên khoảng (−3;−1) thì f(x) nghịch biến
C.Trên khoảng (5;10) thì f(x) nghịch biến
D.Trên khoảng (−1;3) thì f(x) nghịch biến
Tìm các giá trị của tham số m sao cho hàm số \[y' = - 3{x^2} - 2x + m\] nghịch biến trên R?
A.\[m < - 3\]
B. \[m \le - \frac{1}{3}\]
C. \[m < 3\]
D. \[m \ge - \frac{1}{3}\]
Tìm m để hàm số \[y' = \frac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2\] nghịch biến trên khoảng (−2;0).
A.\[m < - \frac{1}{3}\]
B.
C.
D.
Tìm tất cả các giá trị thực của tham số m để hàm số \[y = \frac{{m{x^{}} - 4}}{{2x + m}}\] nghịch biến trên từng khoảng xác định của nó?
A.m=0
B.−2<m<2
</m<2 >
C.m=−1
D.\(\left[ {\begin{array}{*{20}{c}}{m < - 2}\\{m > 2}\end{array}} \right.\)</>
Bất phương trình có tập nghiệm là \[\left[ {a;b} \right].\;\]Hỏi tổng a+b có giá trị là bao nhiêu?
A.5
B.−2
C.4
D.3
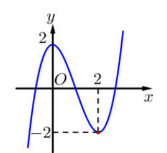
Cho f(x) mà đồ thị hàm số \[y = f\prime (x)\;\] như hình bên. Hàm số \[y = f(x - 1) + {x^2} - 2x\;\] đồng biến trên khoảng?
A.(1;2)
B.(−1;0)
C.(0;1)
D.(−2;−1)
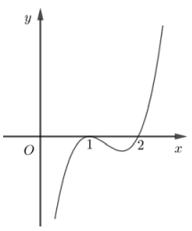
Cho hàm số y=f(x) có đồ thị như hình bên:
Hàm số \[y = - 2f(x)\;\] đồng biến trên khoảng:
A.(1;2)
B.(2;3)
C.(−1;0)
D.(−1;1)
Cho hàm số đa thức f(x) có đạo hàm tràm trên R. Biết f\[\left( 0 \right) = 0\] và đồ thị hàm số \[y = f\prime (x)\]như hình sau.
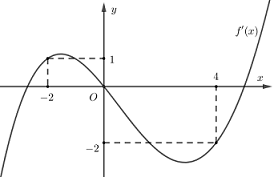
Hàm số \[g\left( x \right) = \left| {4f\left( x \right) + {x^2}} \right|\;\] đồng biến trên khoảng nào dưới đây ?
A. \[\left( {4; + \infty } \right)\]
B.(0;4).
C. \[\left( { - \infty ; - 2} \right)\]
D.(−2;0).
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\)và có đạo hàm \[f\prime (x) = {x^2}(x - 2)({x^2} - 6x + m)\;\] với mọi \[x \in \mathbb{R}\]. Có bao nhiêu số nguyên m thuộc đoạn \[\left[ { - 2019;2019} \right]\;\]để hàm số \[g(x) = f(1 - x)\;\] nghịch biến trên khoảng \[\left( { - \infty ; - 1} \right)?\]
A.2010.
B.2012.
C.2011.
D.2009.
Hàm số \[y = {x^3} - 3{{\rm{x}}^2} + 4\] đồng biến trên:
A.(0;2)
B. \[\left( { - \infty ;0} \right)\;\]và \[\left( {2; + \infty } \right)\]
C. \[\left( { - \infty ;2} \right)\]
D. \[\left( {0; + \infty } \right)\]