Tổng hợp 20 đề thi thử THPT quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 19)

Câu 1:

Đồ thị của hàm số nào dưới đây có hình dạng như hình vẽ bên

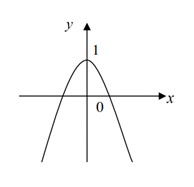
A. $y = x^{4} - 2 x^{2} + 1$

B. $y = x^{4} + 2 x^{2} + 1$

C. $y = - x^{4} + 2 x^{2} + 1$

D. $y = - x^{4} - 2 x^{2} + 1$

Câu 2:

Cho hàm số y=f(x) xác định trên $R / \{- 1; 1\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên

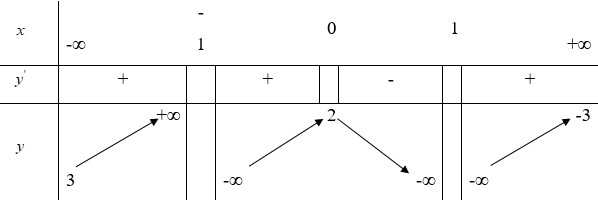
Khẳng định nào dưới đây là sai?

A. Hàm số không có đạo hàm tại x=0 nhưng vẫn đạt cực trị tại x=0

B. Hàm số đạt cực tiểu tại x=1

C. Đồ thị hàm số đã cho có hai đường tiệm cận đứng là các đường thẳng x=-1, x=1

D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng y=-3, y=3

Câu 3:

Tìm giá trị cực tiểu $y_{C T}$ của hàm số $y = x - 5 + \frac{1}{x}$

A. -3

B. 3

C. -5

D. 5

Câu 4:

Tìm nghiệm của phương trình $2^{x + 1} . 5^{x} = 200$

A. $x = 3$

B. $x = \log_{2} 5$

C. $x = 2$

D. $x = \log_{5} 2$

Câu 5:

Cho hàm số f(x) có đạo hàm trên đoạn [2;5], f(2)=9 và f(5)=3. Tính $I = \int_{2}^{5} f' (x) d x$

A. I=6

B. I=12

C. I=-6

D. I=-12

Câu 6:

Cho số phức $z = {(a + b i)}^{2}$ . Để là số thuần ảo thì

A. $a = b = 1$

B. $a = b = - 1$

C. $a = b = 0$

D. $|a| = |b|$

Câu 7:

Cho hàm số $y = \frac{2 x}{x^{2} - 9}$ . Mệnh đề nào dưới đây đúng

A. $H à m s ố đ ồ n g b i ế n t r ê n c á c k h o ả n g (- \infty; - 3) v à (3; + \infty)$

B. $H à m s ố đ ồ n g b i ế n t r ê n c á c k h o ả n g (- \infty; - 3), (- 3; 3) v à (3; + \infty)$

C. $H à m s ố n g h ị c h b i ế n t r ê n c á c k h o ả n g (- \infty; - 3), (- 3; 3) v à (3; + \infty)$

D. $H à m s ố n g h ị c h b i ế n t r ê n c á c k h o ả n g (- \infty; 3)$

Câu 8:

Một họ gồm 3 đường thẳng song song cắt một họ gồm 4 đường thẳng khác song song. Hỏi có tất cả bao nhiêu hình bình hành được tạo thành

A. 16

B. 21

C. 27

D. 18

Câu 9:

Viết phương trình tiếp tuyến của đồ thị hàm số $y = x^{3} - 6 x^{2} + 9 x + 11$ tại điểm cực tiểu

A. y=x+2

B. y=x-2

C. y=1

D. y=-x-2

Câu 10:

Trong các mệnh đề dưới đây, mệnh đề nào đúng

A. $3^{\log_{3} 2} + \log_{3} (9 \sqrt[3]{3}) = \frac{13}{3}$

B. $3^{\log_{3} 2} + \log_{3} (9 \sqrt[3]{3}) = \frac{14}{3}$

C. $3^{\log_{3} 2} + \log_{3} (9 \sqrt[3]{3}) = \frac{17}{3}$

D. $3^{\log_{3} 2} + \log_{3} (9 \sqrt[3]{3}) = \frac{19}{3}$

Câu 11:

Cho $\vec{u} = 3 \vec{i} + 2 \vec{j} + m \vec{k}, \vec{v} = \vec{i} - \vec{k}$ . Tìm m để $\vec{u} \vec{v} = 2$

A. m=0

B=1

C. m=2

D. m=3

Câu 12:

Tìm số hạng đứng chính giữa trong khai triển $P = {(\frac{1}{x^{3}} + \sqrt{x^{5}})}^{n}$ , biết $C_{n + 4}^{n + 1} - C_{n + 3}^{n} = 7 (n + 3)$

A. $\frac{924}{x^{3}}$

B. $924 x^{3}$

C. $\frac{942}{x^{3}}$

D. $942 x^{3}$

Câu 13:

Tìm tập nghiệm Scủa bất phương trình ${(\sqrt{2} + 1)}^{x} \leq {(\sqrt{2} - 1)}^{x}$

A. $S = (- \infty; - 3]$

B. $S = (- \infty; - 3)$

C. $[3; + \infty)$

D. $(3; + \infty]$

Câu 14:

Cho hàm số $f (x) = \frac{\ln x}{x}$ .Tìm nghiệm của phương trình f'(x)=0

A. $1$

B. $e$

C. $\frac{1}{e}$

D. $\frac{1}{e^{2}}$

Câu 15:

Tìm tập xác định D của hàm số $\log_{2} (\log_{3} x)$

A. $D = (0; 1)$

B. $D = (1; + \infty)$

C. $D = (0; + \infty)$

D. $D = (3; + \infty)$

Câu 16:

Tìm nguyên hàm của hàm số $f (x) = x^{e}$

A. $\int f (x) d x = \frac{x^{e}}{\ln x} + C$

B. $\int f (x) d x = \frac{x^{e + 1}}{e + 1} + C$

C. $\int f (x) d x = e . x^{e - 1} + C$

D. $\int f (x) d x = x^{e} + C$

Câu 17:

Biết F(x) là một nguyên hàm của hàm số $f (x) = \frac{x^{3}}{x^{4} + 1}$ và F(0)=1. Tính F(1)

A. $F (1) = \ln 2 + 1$

B. $F (1) = \frac{1}{4} \ln 2 + 1$

C. $F (1) = \ln 2 - 1$

D. $F (1) = \frac{1}{4} \ln 2 - 1$

Câu 18:

Cho $\int_{- 2}^{4} f (x) d x = 2$ .Tính $I = \int_{0}^{6} \frac{1}{2} f (x - 2) d x$

A. I=2

B. I=3

C. I=4

D. I=1

Câu 19:

Cho số phức z thỏa mãn $\frac{2 + i}{1 - i} z = \frac{- 1 + 3 i}{2 + i}$ . Mệnh đề nào dưới đây đúng

A. $z c ó p h ầ n t h ự c b ằ n g \frac{22}{25} v à p h ầ n ả o b ằ n g \frac{4}{25}$

B. $z c ó p h ầ n t h ự c b ằ n g - \frac{22}{25} v à p h ầ n ả o b ằ n g - \frac{4}{25}$

C. $z c ó p h ầ n t h ự c b ằ n g \frac{25}{22} v à p h ầ n ả o b ằ n g \frac{25}{4}$

D. $z c ó p h ầ n t h ự c b ằ n g - \frac{25}{22} v à p h ầ n ả o b ằ n g - \frac{25}{4}$

Câu 20:

Cho số phức z=a+bi $(a, b \in R)$ thỏa mãn $z + 2 \bar{i z} = 3 + 3 i$ . Tính z

A. $|z| = 2$

B. $|z| = \sqrt{5}$

C. $|z| = 5$

D. $|z| = \sqrt{2}$

Câu 21:

Tìm nghiệm phức của phương trình $3 z^{2} + 7 z + 8 = 0$

A. $z = \frac{- 7 \pm i \sqrt{47}}{6}$

B. $z = \frac{7 \pm i \sqrt{47}}{6}$

C. $z = \frac{- 6 \pm i \sqrt{47}}{7}$

D. $z = \frac{6 \pm i \sqrt{47}}{7}$

Câu 22:

Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng $60 °$ . Tính thể tích của khối chóp SABC

A. $\frac{a^{3} \sqrt{3}}{12}$

B. $\frac{a^{3}}{12}$

C. $\frac{a^{3} \sqrt{3}}{4}$

D. $\frac{a^{3} \sqrt{3}}{36}$

Câu 23:

Phương trình $\sqrt{3} c o s x + 2 \sin^{2} (\frac{x}{2} - \frac{π}{4}) = 1$ tương đương với phương trình nào dưới đây

A. $\sin (x - \frac{π}{4}) = 0$

B. $\sin (x - \frac{π}{3}) = 0$

C. $\sin (x + \frac{π}{4}) = 0$

D. $\sin (x + \frac{π}{3}) = 0$

Câu 24:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB vuông cân tại S, tam giác SCD đều. Tính khoảng cách giữa hai đường thẳng SA và BD.

A. $a$

B. $\frac{a}{2}$

C. $\frac{a \sqrt{5}}{5}$

D. $\frac{3 a \sqrt{5}}{20}$

Câu 25:

Cho hình chữ nhật ABCD có AB=a, AC=2a. Tính diện tích xung quanh của hình trụ nhận được khi quay hình chữ nhật quanh cạnh AB

A. $\frac{a^{2} 2 \sqrt{3}}{3}$

B. $\sqrt{3} a^{2}$

C. $2 \sqrt{3} a^{2}$

D. $2 \sqrt{3} π a^{2}$

Câu 26:

Tìm tất cả các giá trị của tham số m để hàm số $y = x + m (\sin x + c o s x)$ đồng biến trên R

A. $m < \frac{- 1}{\sqrt{2}} \cup m > \frac{1}{\sqrt{2}}$

B. $\frac{- 1}{\sqrt{2}} \leq m \leq \frac{1}{\sqrt{2}}$

C. $- 3 < m < \frac{1}{\sqrt{2}}$

D. $m \leq \frac{- 1}{\sqrt{2}} \cup m \geq \frac{1}{\sqrt{2}}$

Câu 27:

Cho tam giác ABC và A(2; 3; -1), B(4; -6; -2) là trọng tâm. Tìm tọa độ của C

A. C(-5; 5; 0)

B. (3; -9; -6)

C. C(-3; 9; 6)

D. C(-3; 9; -6)

Câu 28:

Cho tứ diện ABCD, A(0; 1; 1), B(-1; 0; 2), C(-1; 1; 0), D(2; 1; -1). Tính độ dài đường cao hạ từ đỉnh D

A. $\frac{5}{3}$

B. $\frac{5}{\sqrt{6}}$

C. $\frac{10}{\sqrt{6}}$

D. $\frac{5}{6}$

Câu 29:

Viết phương trình đường thẳng đi qua tâm của mặt cầu $(S) : {(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 3)}^{2} = 4$ và song song với đường thẳng $d : \{\begin{cases} \begin{array}{l} x = 1 + 3 t \\ y = t \end{array} \\ z = 2 - t \end{cases}$

A. $\{\begin{cases} \begin{array}{l} x = 2 + 2 s \\ y = 1 - s \end{array} \\ z = - 1 + 3 s \end{cases}$

B. $\{\begin{cases} \begin{array}{l} x = 2 + 3 s \\ y = - 1 + s \end{array} \\ z = 3 - s \end{cases}$

C. $\{\begin{cases} \begin{array}{l} x = 2 + 2 s \\ y = 1 - s \end{array} \\ z = 1 + 3 s \end{cases}$

D. $\{\begin{cases} \begin{array}{l} x = 2 + 3 s \\ y = - 1 + s \end{array} \\ z = - 3 - s \end{cases}$

Câu 30:

Viết phương trình mặt phẳng (P) đi qua điểm M(1; 2; 3) và cắt các trục tọa độ lần lượt tại A, B, C ở phần dương khác gốc O sao cho tam giác ABC đều

A. (P): x+y+z-6=0

B. (P): x+y+z+6=0

C. (P): x-y-z-6=0

D. (P): x-y-z+6=0

Câu 31:

Cho 3 hàm số y=f(x), y=g(x), $y = \frac{f (x) + 3}{g (x) + 3}$ . Biết hệ số góc các tiếp tuyến của đồ thị các hàm số đã cho tại điểm có hoành độ x=1 là bằng nhau và khác 0. Mệnh đề nào dưới đây đúng

A. $f (1) \leq \frac{- 11}{4}$

B. $f (1) < \frac{- 11}{4}$

C. $f (1) > \frac{- 11}{4}$

D. $f (1) \geq \frac{- 11}{4}$

Câu 32:

Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y = \sqrt{x^{2} + 3} - m (x + 1)$ đồng biến trên khoảng $(- \infty; + \infty)$

A. $[1; + \infty)$

B. $[- 1; 1]$

C. $(- \infty; - 1]$

D. $(- \infty; 1)$

Câu 33:

Tìm m để hàm số $y = \frac{3 x + 2 m}{\sqrt{2 x^{2} + 5}}$ đạt cực đaị tại x=1

A. $m = 2$

B. $m > \frac{15}{4}$

C. $m = \frac{15}{4}$

Câu 34:

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị là hình vẽ bên. Mệnh đề nào dưới đây đúng

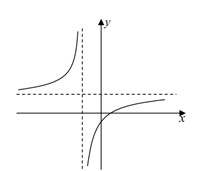
A. ab>0, bd<0

B. ab<0, ad>0

C. ad>0, bd>0

D. ad<0, ab<0

Câu 35:

Tìm hàm số f(x)thỏa mãn $3 x^{2} f' (x) + x^{3} f'' (x) = - 1$ với x khác 0 và $f (1) = 1, f (- 2) = - 1$

A. $f (x) = \frac{1}{x} + \frac{2}{3 x^{2}} + \frac{2}{3}$

B. $f (x) = \frac{1}{x} + \frac{2}{3 x^{2}} - \frac{2}{3}$

C. $f (x) = \frac{1}{x} - \frac{2}{3 x^{2}} - \frac{2}{3}$

D. $f (x) = \frac{1}{x} - \frac{2}{3 x^{2}} + \frac{2}{3}$

Câu 36:

Một bài kiểm tra trắc nghiệm gồm 10 câu hỏi, mỗi câu có 4 phương án để lựa chọn trong đó chỉ có một phương án đúng. Với mỗi câu, nếu chọn phương án đúng thì thí sinh được 5 điểm, nếu chọn phương án sai thì bị trừ 1 điểm. Tính xác xuất để một thí sinh làm bài bằng cách chọn ngẫu nhiên phương án trả lời được 26 điểm.

A. 0,16

B. 0,016

C. 0,036

D. 0,36

Câu 37:

Tìm m để phương trình ${(\frac{1}{2})}^{|x^{2} - 2 x|} = m^{2} - m + 1$ có 4 nghiệm phân biệt

A. 0<m<1

B. m>0

C. 2<m<5

D. m>5

Câu 38:

Biết $\int_{0}^{\frac{π}{4}} \frac{{(1 + \tan x)}^{5}}{c o s^{2} x} d x = \frac{a}{b}$ ; trong đó a, b là 2 số nguyên dương và a/b là phân số tối giản. Mệnhđề nào dưới đây đúng?

A. $a < b$

B. $a b = 1$

C. $a - 10 b = 1$

D. $a^{2} + b^{2} = 1$

Câu 39:

Một đoàn tàu đang chạy với vận tốc 20 km/h giờ thì người lái tàu kéo phanh để giảm tốc độ. Sau khi kéo phanh, tàu chuyển động chậm dần đều với vận tốc V(t)=-40t+20 (km/giờ), trong đó t là khoảng thời gian tính bằng phút kể từ lúc bắt đầu kéo phanh. Hỏi từ lúc kéo phanh đến khi dừng hẳn, tàu còn chuyển động được bao nhiêu

A. 3 km

B. 5,5 km

C. 3,5 km

D. 5 km

Câu 40:

Cho số phức z=x+yi, $(x, y \in R)$ thỏa mãn $z^{3} = 18 + 26 i$ . Tính $T = {(z - 2)}^{2017} + {(4 - z)}^{2017}$

A. $T = 2^{1009}$

B. $T = 2^{1010}$

C. $T = 2^{1011}$

D. $T = 2^{2012}$

Câu 41:

Cho hình chóp SABC có đáy là tam giác vuông tại A, BC=2a, các cạnh bên cùng tạo với đáy một góc $60 °$ . Tính thể tích của khối cầu ngoại tiếp hình chóp SABC

A. $\frac{32 {πa}^{3}}{9 \sqrt{3}}$

B. $\frac{23 {πa}^{3}}{9 \sqrt{3}}$

C. $\frac{32 {πa}^{3}}{9}$

D. $\frac{23 {πa}^{3}}{9}$

Câu 42:

Cho hình nón đỉnh S, chiều cao SO=h, bán kính đáy bằng R. Gọi M là điểm nằm trên đoạn SO , đặtOM=x (0<x<h) Cắt hình nón bằng mặt phẳng (P) đi qua M và vuông góc với SO, thiết diện thu được là đường tròn (C). Tìm x để thể tích của khối nón đỉnh O đáy là hình tròn giới hạn bởi (C) đạt giá trị lớn nhất

A. $x = \frac{h}{2}$

B. $x = \frac{h}{3}$

C. $x = \frac{h}{4}$

D. $x = \frac{h}{5}$

Câu 43:

Cho hình chóp S.ABC có đáy là tam giác vuông tại A, BC=2a, $\hat{A B C} = 60 °$ . Gọi M là trung điểm của BC, SA=SC=SM= $a \sqrt{5}$ . Tính khoảng cách từ điểm S tới mặt phẳng (ABC).

A. a

B. 2a

C. 3a

D. 5a

Câu 44:

Cho 2 điểm A(1; 2; -1), B(7; -2; 3) và cho đường thẳng $d : \frac{x + 1}{3} = \frac{y - 2}{- 2} = \frac{z - 2}{2}$ . Tìm m thuộc d sao cho MA+MB nhỏ nhất

A. M(2; 0; 4)

B. M(2; 0; -4)

C. M(-2; 0; 4)

D. M(0; 2; 4)

Câu 45:

Một người nuôi cá thử nghiệm trong một cái hồ. Qua theo dõi, người đó thấy rằng. Nếu trên mỗi $1 m^{2}$ diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng P(n)=480 -20n (gam). Hỏi để sau một vụ người đó thu hoạch được nhiều cá nhất thì phải thả bao nhiêu con cá trên $1 m^{2}$ diện tích mặt hồ

A. n=12

B. n=15

C. n=21

D. n=51

Câu 46:

Một quả bóng cao su được thả từ độ cao 81m. Mỗi lần chạm đất, quả bóng lại nảy lên hai phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa

A. 504 m

B. 524 m

C. 405 m

D. 425 m

Câu 47:

Với mọi m thì đường thẳng d: y=mx+2 luôn cắt parabol $(P) : y = x^{2} + 1$ tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ . Tìm m để diện tích của hình phẳng giới hạn bởi d và (P) là nhỏ nhất

A. m=0

C. m=4

D. m=1

D. m=2

Câu 48:

Tìm tập hợp các điểm trong mặt phẳng Oxy biểu diễn số phức w=2z+3-i, biết ${|3 z + i|}^{2} = z . \bar{z} + 9$

A. ${(x - 3)}^{2} + {(y + \frac{7}{4})}^{2} = \frac{73}{16}$

B. ${(x + 3)}^{2} + {(y + \frac{7}{4})}^{2} = \frac{73}{16}$

C. ${(x - 3)}^{2} + {(y - \frac{7}{4})}^{2} = \frac{73}{16}$

D. ${(x + 3)}^{2} + {(y - \frac{7}{4})}^{2} = \frac{73}{16}$

Câu 49:

Một người thợ cơ khí cần gò một chiếc thùng bằng tôn cứng, thùng có dạng hình hộp chữ nhật không có nắp và kích cỡ các chiều là x, y, z (dm) đồng thời tỉ lệ x/y=1/3, thể tích của thùng là 18 lít. Hỏi số tiền ít nhất mà người thợ phải bỏ ra để mua tôn là bao nhiêu, biết rằng mỗi đềximét vuông tôn có giá 20 nghìn đồng

A. 720 nghìn

B. 820 nghìn

C. 620 nghìn

D. 920 nghìn

Câu 50:

Trong không gian Oxyz, cho hình chóp tứ giác đều SABCO, S(2; 2; 6), A(4; 0; 0), B(4; 4; 0), C(0; 4; 0). Viết phương trình mặt cầu ngoại tiếp hình chóp SABCO

A. ${(x - 2)}^{2} + {(y - 2)}^{2} + {(z - \frac{7}{3})}^{2} = \frac{121}{9}$

B. ${(x + 2)}^{2} + {(y - 2)}^{2} + {(z - \frac{7}{3})}^{2} = \frac{121}{9}$

C. ${(x - 2)}^{2} + {(y + 2)}^{2} + {(z - \frac{7}{3})}^{2} = \frac{121}{9}$

D. ${(x - 2)}^{2} + {(y - 2)}^{2} + {(z + \frac{7}{3})}^{2} = \frac{121}{9}$

Tổng hợp 20 đề thi thử THPT quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 19)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp 20 đề thi thử THPT quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 19)

CHỌN BỘ SÁCH BẠN MUỐN XEM