Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 6)

Câu 1:

Có bao nhiêu số chẵn có 4 chữ số đôi một khác nhau và lớn hơn 5000?

A .1232.

B.1120.

C.1250.

D.1288.

Câu 2:

Hàm số $y = - x^{3} + 3 x - 5$ đồng biến trên những khoảng nào?

A. $(- \infty; - 1)$

B. $(1; + \infty)$

C. $(- 1; 1)$

D. R.

Câu 3:

Cho khai triển ${(x - 2)}^{80} = a_{0} + a_{1} x + a_{2} x^{2} + ... + a_{80} x^{80}$ .

Tổng $S = 1. a_{1} + 2. a_{2} + 3. a_{3} + ... + 80 a_{80}$ có giá trị là:

A. -70.

B. 80

C. 70

D. -80

Câu 4:

Chọn đáp án đúng:Mỗi cạnh của khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện?

A. không có mặt nào.

B. 3 mặt

C. 4 mặt

D. 2 mặt

Câu 5:

Chọn câu trả lời đúng:

Phương trình $2^{2 x^{2} + 1} - {5.2}^{x^{2} + 3 x} + 2^{6 x + 1} = 0$ có tổng các nghiệm bằng?

A .4.

B. 10.

C. 6.

D. 8.

Câu 6:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = 2a, $\overset{\land}{S B A} = \overset{\land}{S C A} = 90^{0}$ , góc giữa cạnh bên SA với mặt phẳng đáy bằng $60^{0}$ . Tính theo a thể tích khối chóp S.ABC

A. $\frac{a^{3}}{6}$

B. $\frac{4 a^{3} \sqrt{6}}{3}$

C. $\frac{2 a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3}}{4}$

Câu 7:

Cho $\log_{12} 3 = a$ . Khi đó $\log_{24} 18$ có giá trị tính theo a là:

A. $\frac{3 a - 1}{3 - a}$

B. $\frac{3 a + 1}{3 - a}$

C. $\frac{3 a + 1}{3 + a}$

Câu 8:

Chọn câu trả lời đúng:

Phương trình $27^{\frac{x - 1}{x}} {.2}^{x} = 72$ có một nghiệm viết dưới dạng $x = - \log_{a} b$ , với a, b là các số nguyên dương. Khi đó tổng a+b có giá trị là?

A .4.

B. 5.

C. 6.

D. 8.

Câu 9:

Giá trị lớn nhất của hàm số $y = \frac{\sin x + \cos x - 1}{\sin x - \cos x + 3}$ bằng?

A. 3

B. -1

C. $- \frac{1}{7}$

D. $\frac{1}{7}$

Câu 10:

Cho hình chóp S.ABC đáy ABC là tam giác vuông cân với BA = BC = a, SA = a vuông góc với đáy,cosin góc giữa hai mặt phẳng (SAC) và (SBC) bằng:

A. $\frac{1}{2}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{\sqrt{3}}{2}$

Câu 11:

Đồ thị sau đây của hàm số nào?

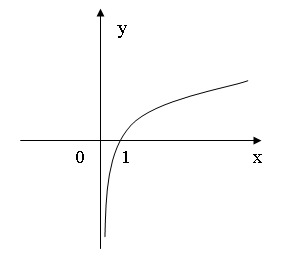
A. $y = 2^{x}$

B. $y = \log_{\frac{1}{2}} x$

C. $y = {(\frac{1}{2})}^{x}$

D. $y = \log_{2} x$

Câu 12:

Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a .Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. M,N,P lần lượt là trung điểm của SB,BC,SD. Tính khoảng cách giữa AP và MN

A. $\frac{3 a}{\sqrt{15}}$

B. $4 \sqrt{15} a$

C. $\frac{3 a \sqrt{5}}{10}$

Câu 13:

Cho đồ thị (C): $y = \frac{\sqrt{x^{2} - 4}}{x + 1}$ , đồ thị (C ) có bao nhiêu đường tiệm cận?

A. 0

B. 1

C. 2

D. 3

Câu 14:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Gọi H và K lần lượt là trung điểm của SB, SD. Tỷ số thể tích $\frac{V_{A O H K}}{V_{S . A B C D}}$ bằng

A. $\frac{1}{12}$

B. $\frac{1}{6}$

C. $\frac{1}{8}$

Câu 15:

Cho a,b là các số hữu tỉ thoả mãn:

$\log_{2} \sqrt[6]{360} = \frac{1}{2} + a \log_{2} 3 + b \log_{2} 5$ .

Khi đó tổng a+b có giá trị là:

A. $\frac{4}{3}$

B. $\frac{2}{3}$

C. $\frac{1}{18}$

D. $\frac{1}{2}$

Câu 16:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết $S D = 2 a \sqrt{3}$ và góc tạo bởi đường thẳng SC và mặt phẳng (ABCD) bằng $30^{0}$ . Tính khoảng cách từ điểm B đến mặt phẳng (SAC).

A. $\frac{2 a}{\sqrt{11}}$

B. $\frac{2 a \sqrt{66}}{11}$

C. $\frac{a \sqrt{15}}{5}$

Câu 17:

Phương trình $|x^{3} - 3 x + 1| = m$ ;(m là tham số) có 6 nghiệm phân biệt khi:

A. $1 < m < 2$ .

B. $m > 2$ .

C. $[\begin{array}{l} m < 1 \\ m > 2 \end{array}$

D. $0 < m < 1$

Câu 18:

Hàm số $y = \frac{1}{3} (m^{2} - 1) x^{3} + (m + 1) x^{2} + 3 x + 5$ đồng biến trên R khi:

A. $m \in \emptyset$

B. $m \geq 2$ .

C. $[\begin{array}{l} m \leq - 1 \\ m \geq 2 \end{array}$

Câu 19:

Chọn câu khẳng định đúng trong các câu sau:

A. Hàm số $y = a^{x}$ đồng biến khi $0 < a < 1$ .

B. Đồ thị hàm số $y = a^{x}$ luôn nằm bên phải trục tung.

C. Đồ thị hàm số $y = a^{x}$ và $y = {(\frac{1}{a})}^{x}$ đối xứng nhau qua trục tung, với $a > 0; a \neq 1$

Câu 20:

Đạo hàm của hàm số $y = 3^{x}$ là:

A. $y' = \frac{- 3^{x}}{\ln 3}$

B. $y' = 3^{x} \ln 3$

C. $y' = \frac{3^{x}}{\ln 3}$

Câu 21:

Với giá trị nào của m thì đồ thị hàm số $y = m x + \sqrt{x^{2} + x + 1}$ có tiệm cận ngang?

A. $m \neq \pm 1$

B. $m = \pm 1$

C. $m \neq \pm 2$

Câu 22:

Cho hàm số $y = x^{4} - 3 x^{2} + 2$ .Chọn khẳng định đúng trong các khẳng định sau:

A. Hàm số có 2 cực đại và 1 cực tiểu.

B. Hàm số có đúng một điểm cực trị.

C. Hàm số luôn đồng biến trên R.

D. Hàm số có 2 cực tiểu và 1 cực đại.

Câu 23:

Cho đồ thị (C): $y = \frac{x + 2}{x - 1}$ , tiếp tuyến với đồ thị (C ) tại một điểm bất kì thuộc (C ) luôn tạo với hai đường tiệm cận của (C ) một tam giác có diện tích không đổi. Diện tích đó bằng:

A. 8

B. 4

C. 10

D. 6

Câu 24:

Cho đồ thị (C): $y = \frac{2 x + 1}{x - 1}$ . Phương trình tiếp tuyến của đồ thị (C ) tại giao điểm của đồ thị (C ) và trục hoành là:

A. $4 x + 3 y - 2 = 0$

B. $4 x - 3 y - 2 = 0$

C. $4 x + 3 y + 2 = 0$

Câu 25:

Chọn câu trả lời đúng:

Phương trình $8^{\frac{2 x - 1}{x + 1}} = 0, 25. {(\sqrt{2})}^{7 x}$ có tích các nghiệm bằng ?

A. $\frac{4}{7}$

B. $\frac{2}{3}$

C. $\frac{2}{7}$

Câu 26:

Hàm số nào sau đây nghịch biến trên khoảng (1;3)?

A. $y = \frac{1}{2} x^{2} - 2 x + 3$

B. $y = \frac{x^{2} + x - 1}{x - 1}$

C. $y = 2 x^{3} - 4 x^{2} + 6 x + 10$ .

D. $y = \frac{2 x + 5}{x - 1}$

Câu 27:

Cho lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân tại B. AB= $a \sqrt{3}$ . Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) là điểm H thuộc cạnh AC sao cho HC=2HA. Mặt bên (ABB’A’) tạo với đáy một góc 60⁰ . Thể tích khối lăng trụ là:

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3}}{3}$

C. $\frac{3 a^{3}}{5}$

D. $\frac{3 a^{3}}{2}$

Câu 28:

Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách 300km, vận tốc của dòng nước là 6(km/h).Giả sử vận tốc bơi của cá khi nước yên lặng là v(km/h).Năng lượng tiêu hao của cá trong t giờ được tính theo công thức $E = c v^{3} t$ ; c là hằng số cho trước, đơn vị của E là Jun. Vận tốc v của cá khi nước đứng yên để năng lượng của cá tiêu hao ít nhất là:

A. $9 (k m / h)$

B. $8 (k m / h)$

C. $10 (k m / h)$

Câu 29:

Một cô giáo dạy văn gửi 200 triệu đồng loại kì hạn 6 tháng vào một ngân hàng với lãi suất 6,9% trên năm.Hỏi sau 6 năm 9 tháng cô giáo nhận được số tiền cả gốc và lãi là bao nhiêu biết cô giáo không rút lãi ở tất cả các kì hạn trước và nếu rút trước ngân hàng sẽ trả lãi suất theo loại lãi suất không kì hạn 0,002% trên ngày?

A. 302088933đ

B. 471688328 đ

C. 311392503 đ

D. 321556228đ.

Câu 30:

Tập xác định của hàm số: $y = {(4 - x^{2})}^{\frac{1}{3}}$ là:

A. $(- \infty; - 2) \cup (2; + \infty)$ .

B. $(- 2; 2)$ .

C. $(- \infty; - 2)$ .

Câu 31:

Tập xác định của hàm số: $y = \log_{3} (x^{2} - 4 x + 3)$ là:

A. $(- \infty; 1) \cup (3; + \infty)$ .

B . $(1; 3)$ .

C. $(- \infty; 1)$ .

Câu 32:

Chọn câu trả lời đúng:

Phương trình $3^{2 x} - {4.3}^{x + 1} + 27 = 0$ có tổng các nghiệm bằng ?

A .0

B. 1

C. 2

D. 3

Câu 33:

Xếp ngẫu nhiên 7 học sinh nam và 3 học sinh nữ ngồi xung quanh một bàn tròn. Xác suất để các học sinh nữ luôn ngồi cạnh nhau là:

A. $\frac{3}{10}$

B. $\frac{1}{12}$

C. $\frac{5}{32}$

D. $\frac{5}{42}$

Câu 34:

Đồ thị hàm số $y = - x^{4} + 2 x^{2}$ là đồ thị nào sau đây?

A.

B.

C.

D.

Câu 35:

Cho hàm số $y = x^{3} + 3 x^{2} - 9 x - 2017$ . Chọn khẳng định đúng trong các khẳng định sau:

A. Hàm số đồng biến trên khoảng $(- 3; 1)$ .

B. Hàm số đạt cực tiểu tại x=-3; đạt cực đại tại x=1

C. Hàm số đạt cực đại tại x=-3; đạt cực tiểu tại x=1.

D. Đồ thị hàm số cắt Ox tại ba điểm.

Câu 36:

Khối lập phương thuộc loại khối đa diện nào? Chọn câu trả lời đúng.

A {3;3}.

B.{4;3}.

C. {3;4}.

D.{5;3}.

Câu 37:

Cho một hình đa diện. Khẳng định nào sau đây sai?

A. Mỗi mặt có ít nhất 3 cạnh.

B. Mỗi đỉnh là đỉnh chung của ít nhất 3 cạnh.

C. Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt.

D. Mỗi cạnh là cạnh chung của ít nhất 3 mặt.

Câu 38:

Đồ thị hàm số $y = x^{3} - 3 m x^{2} + 9 x - 7$ cắt trục hoành tại 3 diểm phân biệt có hoành độ lập thành cấp số cộng khi:

A. $[\begin{array}{l} m = 1 \\ m = \frac{- 1 \pm \sqrt{15}}{2} \end{array}$

B. $m = \frac{- 1 + \sqrt{15}}{2}$

C. $m = \frac{- 1 - \sqrt{15}}{2}$

D. m = 1

Câu 39:

Cho hàm số y=f(x) liên tục và có đạo hàm tới cấp hai trên a,b ; $x_{0} \in (a; b)$ . Chọn khẳng định đúng trong các khẳng định sau:

A. Nếu $\{\begin{cases} f' (x_{0}) = 0 \\ f'' (x_{0}) < 0 \end{cases}$ thì $x_{0}$ là một điểm cực tiểu của hàm số

B. Nếu $\{\begin{cases} f' (x_{0}) = 0 \\ f'' (x_{0}) \neq 0 \end{cases}$ thì $x_{0}$ là một điểm cực trị của hàm số.

C. Nếu $\{\begin{cases} f' (x_{0}) = 0 \\ f'' (x_{0}) > 0 \end{cases}$ thì $x_{0}$ là một điểm cực đại của hàm số

D. A, B, C đều sai.

Câu 40:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB=AC= $a \sqrt{2}$ . A’B tạo với đáy góc $60^{0}$ . Thể tích khối lăng trụ là:

A. $a^{3} \sqrt{6}$

B. $\frac{3 a^{3} \sqrt{3}}{2}$

C. $4 a^{3} \sqrt{6}$

D. $\frac{5 a^{3}}{3}$

Câu 41:

Cho đồ thi (C): $y = - x^{3} - x - 1$ và đường thẳng $d : y = - x + m^{2}$ ;m là tham số .Chọn khẳng định đúng trong các khẳng định sau:

A. Với $\forall m$ ,đồ thị (C) luôn cắt d tại 3 điểm phân biệt.

B. Với $\forall m$ ,đồ thị (C) luôn cắt d tại 2 điểm phân biệt

C. Với $\forall m$ ,đồ thị (C) luôn cắt d tại đúng 1 điểm duy nhất có hoành độ âm.

D. Với $\forall m$ ,đồ thị (C) luôn cắt d tại đúng 1 điểm duy nhất.

Câu 42:

Cho hình chóp S.ABC có SA=SB=SC, tam giác ABC là tam giác vuông tại B, AB=a; BC= $a \sqrt{3}$ , mặt bên (SBC) tạo với đáy góc $60^{0}$ . Thể tích khối chóp S.ABC là:

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3}}{3}$

C. $\frac{2 a^{3}}{3}$

Câu 43:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đèu cạnh $a \sqrt{3}$ . A’B = 3A. Thể tích khối lăng trụ là:

A. $\frac{7 a^{3}}{2}$

B. $\frac{9 a^{3} \sqrt{2}}{4}$

C. $6 a^{3}$

D. 7a³

Câu 44:

Cho hình lăng trụ ABC.A'B'C' có $A A' = \frac{a \sqrt{10}}{4}$ , AC = $a \sqrt{2}$ , BC = a, $\hat{A C B} = 135^{0}$ . Hình chiếu vuông góc của C' lên mặt phẳng (ABC) trùng với trung điểm M của AB. Tính góc tạo bởi đường thẳng C'M với mặt phẳng (ACC' A') ?

A. $90^{0}$

B. $60^{0}$

C. $45^{0}$

D. $30^{0}$

Câu 45:

Phương trình $\sin 5 x + \sin 9 x + 2 \sin^{2} x - 1 = 0$ có họ một họ nghiệm là:

A. $x = \frac{π}{42} + \frac{k 2 π}{7}$

B. $x = \frac{π}{42} + \frac{k 2 π}{3}$

C. $x = \frac{π}{5} + k 2 π$

Câu 46:

Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng $60^{0}$ . Tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a .

A. $\frac{3 a}{\sqrt{5}}$

B. $\frac{a \sqrt{3}}{4}$

C. $\frac{a \sqrt{3}}{5}$

Câu 47:

Đồ thị sau đây là của hàm số y=f'(x). Khi đó hàm số y=f(x) có bao nhiêu điểm cực trị?

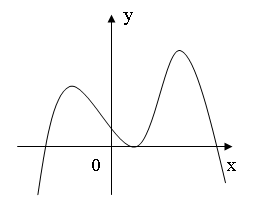
A .0

B.1

C.2

D.3

Câu 48:

Cho hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 1) x - m^{3} + 4 m - 1$ .

Đồ thị hàm số có hai điểm cực trị tạo với gốc toạ độ O một tam giác vuông tại O khi:

A. $[\begin{array}{l} m = 1 \\ m = - 2 \end{array}$

B. $[\begin{array}{l} m = - 1 \\ m = 2 \end{array}$

C. m = -1

D. m = -2.

Câu 49:

Chọn câu trả lời đúng:

Phương trình ${(\frac{1}{7})}^{x^{2} - 2 x - 3} = 7^{x - 1}$ có bao nhiêu nghiệm?

A .0

B. 1

C. 2

D. 3

Câu 50:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a \sqrt[]{3}$ , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là:

A. $\frac{9 a^{3} \sqrt{3}}{2}$

B. $\frac{a^{3}}{2}$

C. $\frac{3 a^{3}}{2}$

Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 6)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 6)

CHỌN BỘ SÁCH BẠN MUỐN XEM