Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 12)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến the vecto biến M thành A thì v bằng
A.
B.
C.
D.
Tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số
A. 5
B. 4
C. 8
D. 10
Cho f(x)=, biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)=2018. Tính F(2)
A. F(2) = 5+2017
B. F(2) = 4+2017
C. F(2) = 3+2017
D. F(2)= 2022
Tính nguyên hàm
A.
B.
C.
D.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
A. miny= --1;maxy= +1
B. miny= --1;maxy= -1
C. miny= -;maxy= -1
D. miny= --2;maxy= -1
Tìm tất cả các khoảng đồng biến của hàm số
A. (0;2)
B.
C. và
D.
Tìm tất cả các giá trị thực của m để phương trình có nghiệm thực
A.
B.
C.
D.
Gọi M, N lầm lượt là các điểm cực đại và điểm cực tiểu của đồ thị hàm số . Tính độ dài đoạn MN
A. MN=20
B. MN=2
C. MN=4
D. MN=
Hàm số đạt cực tiểu tại x=2 khi
A. m>0
B. m<0
C. m=0
D.
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Khẳng định nào sau đây đúng?
A. Nếu có số thực M thoả mãn thì M là giá trị lớn nhất của hàm số y=f(x) trên đoạn [a;b]
B. Nếu sao cho [a;b] thì m là giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [a;b].
C. Nếu có số thực m thoảm mãn thì là giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [a;b]
D. Nếu có số thực M thoảm mãn thì M là giá trị lớn nhất của hàm số y=f(x) trên đoạn [a;b]
Với giá trị nào của m sau đây thì hàm số không có tiệm cận đứng?
A. m= 2
B. m=
C. m= -1/2
D. m= -1/
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
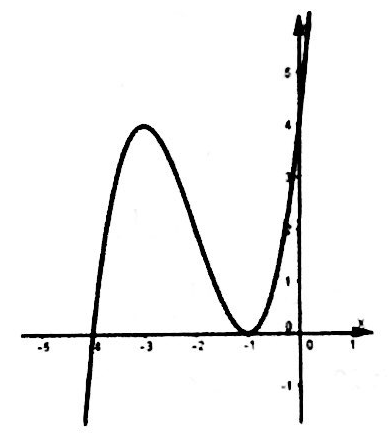
A.
B.
C.
D.
Cho ba số phức thỏa mãn và . Tính
A. z= 0
B. z= -1
C. z= 1
D. z= -2
Tìm tất cả các giá trị thực của tham số m để phương trình có 3 nghiệm thực phân biệt
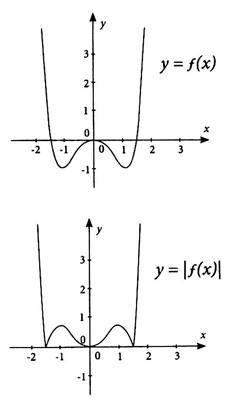
A. 0<m<1
B. m=0
C. m=1
D. m>1
Hai đường cong và tiếp xúc nhau tại điểm . Tìm phương trình đường thẳng d là tiếp tuyến chung của tại điểm
A. y= - 5/4
B. y= 2x-9/4
C. y= 5/4
D. y= 2x+9/4
Một gia đình xây cái bể hình trụ có thể tích 100. Đáy bể làm bằng bê tông 100.000đ/. Phần thân làm bằng tôn giá 90.000đ/. Phần nắp làm bằng nhôm giá 120.000đ/. Hỏi chi phí xây dựng bể đạt mức thấp nhất thì tỉ số giữa chiều cao h và bán kính đáy R của bể là bao nhiêu
A. h/R= 22/9
B. h/R= 9/22
C. h/R= 23/9
D. h/R= 7/3
Hàm số đạt cực trị tại điểm
A. x=0
B. x=
C. x= 1/
D. x= 0; x= 1/
Cho hàm số . Khẳng định nào sau đây sai
A. Hàm số có tập xác định D=R\{0}
B. Hàm số có đạo hàm cấp 1 là y'=
C. Hàm số nghịch biến trên khoảng xác định
D. Hàm số nhận mọi giá trị thuộc R
Tìm tập nghiệm S của bất phương trình
A. S=[ 0;1)[2;3]
B. S=[0;1)[ 2;3]
C. S=[0;1][2;3]
D. S=[0;1][ 2;3]
Giải phương trình
A. x=0 và x=3
B. x=0
C. x=3
D. Vô nghiệm
Cho hàm số . Tìm m để hàm số đồng biến trên khoảng (1;2)
A.
B.
C.
D.
Cho a, b là các số thực thuộc khoảng và thỏa mãn điều kiện cota-tan(-b)=a-b. Tính giá trị của biểu thức
A. P=5
B. P=2
C. P=4
D. P=6
Cho hình phẳng (H) giới hạn bởi các đường y= x lnx;y =0;x= e. Tính thể tích V của khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Ox
A.
B.
C.
D.
Trong không gian cho hình trụ có bán kính đáy R=3, chiều cao h=5. Tính diện tích toàn phần của hình trụ đó
A. =48
B. =30
C. =18
D. =39
Trong không gian cho tam giác ABC vuông tại A có AB=a,AC=a. Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB
A. l= a
B. l= a
C. l=(1+)a
D. l=2a
Trên tập số phức C, cho phương trình (). Khẳng định nào sau đây sai
A. Tổng hai nghiệm của phương trình bằng -b/a.
B. thì phương trình vô nghiệm.
C. Phương trình luôn có nghiệm.
D. Tích hai nghiệm của phương trình là c/a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a. Tính thể tích V của khối chóp S.ABCD
A. V=
B. V=
C. V=
D. V=1/3
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w=(3-4i)z-1+2i là đường tròn tâm I, bán kính R. Tìm tọa độ tâm I và bán kính R của đường tròn đó
A. I(1;2); R=
B. I(1;-2); R=5
C. I(1;2); R=5
D. I(-1;2); R=5
Trong không gian Oxyz, cho điểm I(2;6;-3) và các mặt phẳng :z+2=0. Tìm mệnh đề sai
A.
B.
C.
D.
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x+2y+z-4=0 và đường thẳng d:. Viết phương trình chính tắc của đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d
A.
B.
C.
D.
Trong không gian Oxyz, cho tứ diện ABCD với A(1;6;2), B(5;1;3), C(4;0;6),D(5;0;4), viết phương trình mặt cầu tâm D tiếp xúc với mặt phẳng (ABC)
A.
B.
C.
D.
Trong không gian Oxyz, cho ba điểm A(2;-1;4), B(-2;2;-6), C(6;0;-1). Viết phương trình mặt phẳng (ABC).
A. -5x-60y-16z-16 = 0
B. 5x-60y-16z-6 = 0
C. 5x+60y+16z-14 = 0
D. 5x+60y+16z+14 = 0
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;0;1), B(1;2;1), C(4;1;-2) và mặt phẳng (P):x+y+z=0. Tìm trên (P) điểm M sao cho đạt giá trị nhỏ nhất. Khi đó M có tọa độ:
A. M(1;1;-1)
B. M(1;1;1)
C. M(1;2;-1)
D. M(1;0;-1)
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình 2x-y+2z+1=0, đường thẳng d có phương trình . Gọi là góc giữa đường thẳng d và mặt phẳng (P). Tính giá trị cos
A.
B.
C.
D.
Cho hình chóp đều S.ABCD, có cạnh đáy bằng 2a. Mặt bên hình chóp tạo với đáy một góc bằng . Mặt phẳng (P) chứa AB đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M, N. Tính theo a thể tích V khối chóp S.ABMN
A.
B.
C.
D.
Cho hình lăng trụ có tất cả các cạnh đều bằng a, đáy là hình lục giác đều, góc tạo nên bởi cạnh bên và đáy bằng . Tính thể tích V khối lăng trụ
A.
B.
C.
D. V=
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp đáy một góc . Khoảng cách giữa SA và BD theo a là
A.
B.
C.
D.
Cho hai số phức thỏa mãn và . Giá trị lớn nhất của là
A. 20
B. 40
C. 30
D.
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB= a, và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
A.
B. V= 10/9
C. V= 4/3
D. V= 10/9
Số nghiệm của phương trình (1) là
A. 1007
B. 1008
C. 2016
D. 2017
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn: và . Tính
A. I=8
B. I=9
C. I=6
D. I=7
Một đám vi trùng ngày thứ t có số lượng là N(t). Biết rằng N'(t)= và lúc đầu đám vi trùng có 250000 con. Tính số lượng vi trùng sau 10 ngày (làm tròn đến hàng đơn vị)
A. 264334 con
B. 257167 con
C. 258959 con
D. 253584 con
Cho mặt cầu S(O;R) và (P) cách O một khoảng bằng h (0<h<R). Gọi (L) là đường tròn giao tuyến của mặt cầu (S) và (P) có bán kính r. Lấy A là một điểm cố định thuộc (L). Một góc vuông xAy trong (P) quay quanh điểm A. Các cạnh Ax, Ay cắt (L) ở C và D. Đường thẳng đi qua A và vuông góc với (P) cắt mặt cầu ở B. Diện tích ΔBCD lớn nhất bằng
A.
B.
C.
D.
Khi triển A==. Biết rằng . Hỏi bằng
A. – 33265
B. – 34526
C. – 6464
D. – 8364
Cho có 4 đường thẳng song song với BC, 5 đường thẳng song song với AC, 6 đường thẳng song song với AB. Hỏi 15 đường thẳng đó tạo thành bao nhiêu hình thang (không kể hình bình hành).
A. 360
B. 2700
C. 720
D. Kết quả khác
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)>3. Biết với m>0. Tính ?
A. 2
B. 1
C. 3
D. 4
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)>3. Biết với m>0. Tính ?
A. 2
B. 1
C. 3
D. 4
Cho hàm số y=f(x) có đạo hàm , biết hàm số luôn có hai cực với a, b là các số thực không âm thỏa mãn . Tìm giá trị lớn nhất của biểu thức P = 2a+b
A. 1
B. 9
C. 8
D. 6
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu thì bốc ra 2 bi từ bình 1, còn nếu x+y < 5 thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. 29/36
B. 5/6
C. 13/72
D. 59/72
Một người gửi vào ngân hàng số tiền 20 triệu với lãi suất 1,65%/quý (một quý có 3 tháng) và không lấy lãi đến kì hạn lấy lãi. Hỏi sau bao lâu người đó được 30 triệu (cả vốn lẫn lãi) từ số vốn ban đầu? (giả sử lãi suất không thay đổi)
A. 6 năm 3 quý
B. 7 năm
C. 6 năm 1 quý
D. 6 năm 2 quý