Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 16)

Câu 1:

Phần thực và phần ảo của các số phức $\frac{3}{1 + 2 i}$ là:

A. $\frac{3}{5}$ và $\frac{- 6}{5}$

B. $\frac{1}{5}$ và $\frac{- 2}{5}$

C. $\frac{7}{5}$ và $\frac{6}{5}$

D. $\frac{1}{2}$ và 3

Câu 2:

Viết phương trình mặt phẳng (P) chứa điểm A và đường thẳng d. A(2;-3;1) và d: $\{\begin{cases} x = 4 + 2 t \\ y = 2 - 3 t \\ z = 3 + t \end{cases}$ .

A. 11x+2y+16z-32=0

B. 11x-2y+16x-44=0

C. 11x+2y-16z=0

D. 11x-2y-16z-12=0

Câu 3:

Giả sử x,y là các số thực dương. Mệnh đề nào sau đây là sai?

A. $l o g_{2} (x + y) = l o g_{2} x + l o g_{2} y$

B. $l o g_{2} \sqrt{x y} = \frac{1}{2} (l o g_{2} x + l o g_{2} y)$

C. $l o g_{2} x y = l o g_{2} x + l o g_{2} y$

D. $l o g_{2} \frac{x}{y} = l o g_{2} x - l o g_{2} y$

Câu 4:

Cho $\sin α = - \frac{1}{2}, π < α < \frac{3 π}{2}$ .Tính A = 4 $s i n^{2} α - 2 c o s α + 3 c o t α$ :

A. $\frac{- \sqrt{3}}{2}$

B. 1+ $4 \sqrt{3}$

C. $- \frac{\sqrt{3} + 2}{2}$

D. $\frac{4 \sqrt{3}}{3}$

Câu 5:

Tìm m để hàm số $y = \sqrt{5 \sin 4 x - 6 \cos 4 x + 2 m - 1}$ xác định với mọi x

A. $m \geq 1$

B. $m \geq \frac{\sqrt{61} - 1}{2}$

C. $m \geq \frac{\sqrt{61} + 1}{2}$

D. $m < \frac{\sqrt{61} + 1}{2}$

Câu 6:

Mệnh đề nào sau đây là đúng ?

A. $\int \frac{d x}{\sqrt{x}} = 2 \sqrt{x} + C$

B. $\int \frac{d x}{x^{2}} = \frac{1}{x} + C$

C. $\int \frac{d x}{x + 1} = \ln |x| + C$

D. $\int 2^{x} = 2^{x} + C$

Câu 7:

Tập xác định của hàm số $y = (x - 1)^{\frac{1}{2}}$ là

A. $D = [1; + \infty)$

B. $D = (1; + \infty)$

C. $D = (- \infty; 1)$

D. $D = (0; 1)$

Câu 8:

Tìm tọa độ điểm M^'đối xứng với M qua đường thẳng d biết M(2;-4;1), d: $\{\begin{cases} x = 3 t - 1 \\ y = t + 2 \\ z = 4 t + 5 \end{cases}$

A. M'(7;7;5)

B. M'(-7;7;5)

C. M' $(- \frac{5}{2}; \frac{3}{2}; 3)$

D. M' $(\frac{5}{2}; \frac{3}{2}; 3)$

Câu 9:

Giá trị nào của m thì hàm số $y = \frac{x + m}{x - 2}$ nghịch biến trên từng khoảng xác định là:

A. m < -2

B. $m \leq - 2$

C. $m \geq - 2$

D. m > -2

Câu 10:

Vật thể nào trong các vật thể sau không phải là khối đa diện.

A.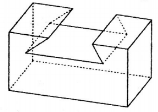

B.

C.

D.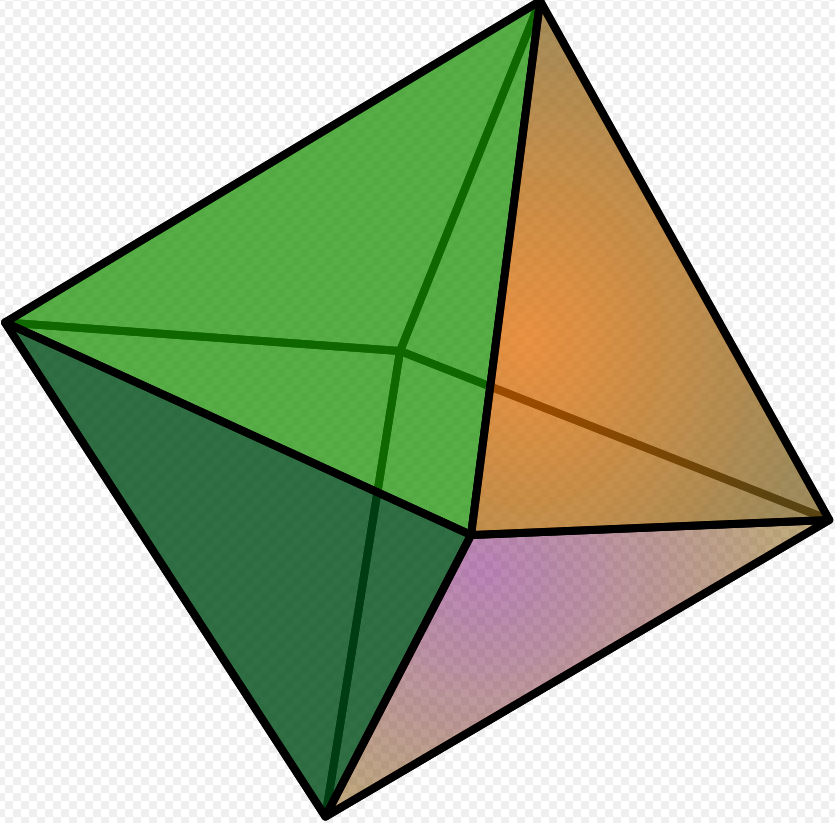

Câu 11:

$\frac{(1 - 2 \sin x) \cos x}{(1 + 2 \sin x) (1 - \sin x)} = 1 .$ Tổng tất cả các nghiệm thuộc đoạn $(- 2 π, 0)$ là:

A. $\frac{- 5 π}{6}$

B. $\frac{- 5 π}{2}$

C. $- 2 π$

D. $\frac{- 11 π}{6}$

Câu 12:

Cho hàm số $y = \frac{x}{2^{x}}$ . Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho có cả điểm cực đại và điểm cực tiểu.

B. Hàm số đã cho có điểm cực tiểu.

C. Hàm số đã cho có điểm cực đại.

D. Hàm số đã cho không có điểm cực trị.

Câu 13:

Tại siêu thị XQ đang có chương trình giải thưởng lá phiếu may mắn cho 4 khách hàng mua với đơn giá trên 10 triệu đồng. Trên mỗi phiếu có một màu riêng biệt là đỏ, vàng và xanh. Vào thời điểm cuối ngày tổng kết, có tất cả là 10 người phiếu đỏ, 8 người phiếu vàng và 6 người phiếu xanh. Trưởng phòng chi nhánh sẽ tiến hành chọn ngẫu nhiên những người được thưởng. Xác suất những người được giải có đủ cả ba loại lá phiếu là:

A. $\frac{120}{253}$

B. $\frac{143}{237}$

C. $\frac{163}{251}$

D. $\frac{191}{325}$

Câu 14:

Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(-1)>0<f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x),y=0,x=-1 và x=1. Mệnh đề nào sau đây đúng?

A. $S = \int_{- 1}^{0} f (x) d x + \int_{0}^{1} | f (x) | d x$

B. $S = \int_{- 1}^{1} | f (x) | d x$

C. $S = \int_{- 1}^{1} f (x) d x$

D. $S = |\int_{- 1}^{1} f (x) d x|$

Câu 15:

Biết x,y là nghiệm của hệ sau $\{\begin{cases} C_{x}^{y} - C_{x}^{y + 1} = 0 \\ 4 C_{x}^{y} + 5 C_{x}^{y - 1} = 0 \end{cases}$ . Giá trị của x + y là

A. 26

B. 25

C. 27

D. 28

Câu 16:

Tìm tất cả các giá trị của tham số m để hàm số $y = - x^{3} + m x^{2} - x$ có 2 điểm cực trị

A. $| m | \geq 2 \sqrt{3}$

B. $| m | > 2$

C. $| m | > \sqrt{3}$

D. $| m | \geq \sqrt{3}$

Câu 17:

Cho hàm số y=f(x) có đạo hàm $f' (x) = x^{2} (x^{2} - 4)$ , $x \in R$ . Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho có 2 điểm cực trị.

B. Hàm số đã cho đạt cực đại tại x = 2

C. Hàm số đã cho có 3 điểm cực trị.

D. Hàm số đã cho đạt cực tiểu tại x = -2

Câu 18:

Tính tổng S = $\frac{- C_{n}^{1}}{2.3} + \frac{2 C_{n}^{2}}{3.4} + \frac{3 C_{n}^{3}}{4.5} +$ $. . . + \frac{{(- 1)}^{n} n C_{n}^{n}}{(n + 1) (n + 2)}$

A. $\frac{n}{(n + 1) (n + 2)}$

B. $\frac{- 2 n}{(n + 1) (n + 2)}$

C. $\frac{- n}{(n + 1) (n + 2)}$

D. $\frac{2 n}{(n + 1) (n + 2)}$

Câu 19:

Trong khong gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(0;0;0);B(3;0;0); D(0;3;0);D'(0;3;-3). Tọa độ trọng tâm của tam giác A’B’C’ là

A. (1;1;-2)

B. (2;1;-1)

C. (1;2;-1)

D. (2;1;-2)

Câu 20:

Trong không gian Oxyz cho mp (P): x + 2y - z + 5 = 0 và đường thẳng $d : \frac{x + 1}{2} = y + 1 = z - 3$ . Tính góc $α$ giữa đường thẳng d và mp (P).

A. $α$ = $60 °$

B. $α$ = $45 °$

C. $α$ = $30 °$

D. $α$ = $90 °$

Câu 21:

Cho cấp số nhân $(u_{n})$ có $S_{2} = 4; S_{3} = 13$ . Khi đó $S_{5}$ bằng:

A. 121 hoặc $\frac{35}{16}$

B. 141 hoặc $\frac{183}{16}$

C. 144 hoặc $\frac{185}{16}$

D. 121 hoặc $\frac{181}{16}$

Câu 22:

Cho cấp số nhân $(u_{n})$ có $S_{2} = 4; S_{3} = 13$ . Khi đó $S_{5}$ bằng:

A. 121 hoặc $\frac{35}{16}$

B. 141 hoặc $\frac{183}{16}$

C. 144 hoặc $\frac{185}{16}$

D. 121 hoặc $\frac{181}{16}$

Câu 23:

Phương trình $(m^{4} + m + 1) x^{2011} + x^{5} - 32 = 0$

(1) Phương trình trên có ít nhất một nghiệm dương với mọi giá trị của m.

(2) Phương trình trên vô nghiệm

(3) Phương trình trên có nghiệm với mọi m

Chọn đáp án đúng

A. Cả 3 đều sai

B. Cả 3 đều đúng

C. Chỉ có (1) đúng

D. (1),(3) Đúng

Câu 24:

Tính đạo hàm của các hàm số $y = \frac{\sin^{3} x + \cos^{3} x}{s i n x + c o s x}$

A. $y' = - \cos^{2} x + \sin^{2} x$

B. y' = 1

C. y' = 0

D. $y' = - \cos^{2} x - \sin^{2} x$

Câu 25:

Cho hàm số y=f(x) liên tục trên R và thỏa mãn $\int_{1}^{e} \frac{f (\ln x)}{x} d x = e$ . Mệnh đề nào sau đây là đúng?

A. $\int_{0}^{1} f (x) d x = 1$

B. $\int_{0}^{1} f (x) d x = e$

C. $\int_{0}^{e} f (x) d x = 1$

D. $\int_{0}^{e} f (x) d x = e$

Câu 26:

Tìm tham số m để đồ thị hàm số $y = 9 x^{4} - 2 (m - 1) x^{2} -$ $3 m^{2} + 3 m + 1$ có ba điểm cực trị và ba điểm cực trị đó tạo thành tam giác có 1 góc bằng $60 °$ ?

A. m = 1

B. m = 4

C. m = 3

D. m = 2

Câu 27:

Một hình nón có đỉnh S, đường cao SO, gọi A, B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ AB đến O bằng a và góc $\hat{S A O} = 30 °,$ $\hat{S A B} = 60 °$ . Tính diện tích xung quanh nón.

A. $S_{x q} = 2 {πa}^{2} \sqrt{3}$

B. $S_{x q} = 3 {πa}^{2} \sqrt{3}$

C. $S_{x q} = {πa}^{2} \sqrt{3}$

D. $S_{x q} = 4 {πa}^{2} \sqrt{3}$

Câu 28:

Tập xác định D của hàm số $y = l o g_{2} (l n^{2} x - 1)$ là:

A. D = $(0; \frac{1}{e}) \cup (e; + \infty)$

B. D = $(0; + \infty)$

C. D = $(e; + \infty)$

D. D = $(0; \frac{1}{e}) \cup (e; + \infty); (0; \frac{1}{e})$

Câu 29:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $△$ nằm trong mặt phẳng $(α) : x + y + z - 3 = 0$ đồng thời đi qua điểm M(1;2;0) và cắt đường thẳng D: $\frac{x - 2}{2} = \frac{y - 2}{1} = \frac{z - 3}{1}$ . Một vecto chỉ phương của $△$ là

A. $\vec{u}$ (1; -1; -2)

B. $\vec{u}$ (1; 0; -1)

C. $\vec{u}$ (1; 1; -2)

D. $\vec{u}$ (1; -2; 1)

Câu 30:

Diện tích và chu vi của một hình chữ nhật ABCD (AB > AD) theo thứ tự là $2 a^{2}$ và 6a. Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này.

A. $4 π a^{3}; 4 π a^{2}$

B. $2 π a^{3}; 4 π a^{2}$

C. $2 π a^{3}; 2 π a^{2}$

D. $4 π a^{3}; 2 π a^{2}$

Câu 31:

Cho hình chóp S.ABC có đáy ABCD là tam giác vuông tại C, AB= $\sqrt{5}$ a,AC=a. Cạnh SA=3a và vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng

A. $a^{3}$

B. $\frac{\sqrt{5}}{2} a^{3}$

C. $2 a^{3}$

D. $3 a^{3}$

Câu 32:

Tìm tất cả các giá trị của tham số m để phương trình $x - \frac{1}{l o g_{3} (x + 1)} = m$ có hai nghiệm phân biệt

A. -1 < m $\neq$ 0

B. m > -1

C. không tồn tại m

D. -1 < m < 0

Câu 33:

Cho hàm số $y = l o g_{a} x v à y = l o g_{b} x$ có đồ thị như hình vẽ bên. Đường thẳng x=7 cắt trục hoành, đồ thị hàm số $y = l o g_{a} x$ và $y = l o g_{b} x$ lần lượt tại H, M và N. Biết rằng HM=MN. Mệnh đề nào sau đây là đúng?

A. a = 7b

B. $a = b^{2}$

C. $a = b^{7}$

D. a = 2b

Câu 34:

Cho mệnh đề:

1) Mặt cầu có tâm I(1;0;-1), đường kính bằng 8 là: $(x - 1)^{2} + y^{2} + (z + 1)^{2} = 16$

2) Mặt cầu có đường kính AB với A=(-1;2;1),B=(0;2;3) là: $(x + \frac{1}{2})^{2} + (y - 2)^{2}$ $+ (z - 2)^{2} = \sqrt{\frac{5}{4}}$

3) Mặt cầu có tâm O(0;0;0) và tiếp xúc với mặt cầu (S) có tâm (3;-2;4), bán kính bằng 1 là: $x^{2} + y^{2} + z^{2} = 30 \pm 2 \sqrt{29}$

Số mệnh đề đúng là bao nhiêu:

A. 2

B. 1

C. 3

D. 0

Câu 35:

Tìm tất cả các giá trị của tham số a để đồ thị hàm số $y = \frac{x^{2} + a}{x^{3} + a x^{2}}$ có 3 đường tiệm cận

A. a < 0, $a \neq 1$

B. a > 0

C. $a \neq 0, a \neq \pm 1$

D. $a \neq 0, a \neq - 1$

Câu 36:

Tìm tất cả các giá trị của tham số m để hàm số $y = (m^{2} - 1) x^{4} - 2 m x^{2}$ đồng biến trên khoảng $(1; + \infty)$

A. $m \leq - 1$

B. m = -1 hoặc $m > \frac{1 + \sqrt{5}}{2}$

C. $m \leq - 1$ hoặc $m \geq \frac{1 + \sqrt{5}}{2}$

D. $m \leq - 1$ hoặc m > 1

Câu 37:

Tìm tất cả các giá trị của tham số m để hàm số $y =$ $\frac{1}{m l o g_{3}^{2} x - 4 l o g_{3} x + m + 3}$ xác định trên khoảng $(0; + \infty)$ là

A. $m \in (- 4; 1)$

B. $m \in [1; + \infty)$

C. $m \in (- \infty; - 4) \cup (1; + \infty)$

D. $m \in (1; + \infty)$

Câu 38:

Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với các kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này (phần tô màu làm bằng thủy tinh). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát gần nhất với giá trị nào trong các giá trị sau

A. 711,6 $c m^{3}$

B. 1070,8 $c m^{3}$

C. 602,2 $c m^{3}$

D. 6021,3 $c m^{3}$

Câu 39:

Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $z_{1} + z_{2}$ $= \frac{3}{5} + \frac{4}{5} i, | z_{1} - z_{2} | = \sqrt{3}$ và biểu thức $P = 4 | z_{1} |^{3} + 4 | z_{2} |^{3}$ $- 3 | z_{1} | - 3 | z_{2} | + 5$ đạt giá trị nhỏ nhất. Tính $| z_{1} | + | z_{2} |$ .

A. 3

B. $\frac{3}{4}$

C. 2

D. 1

Câu 40:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng $Δ : \frac{x}{1} = \frac{x + 3}{1} = \frac{z}{2}$ . Biết rằng mặt cầu (S) có bán kính bằng $2 \sqrt{2}$ và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính bằng 2. Tìm tọa độ tâm I

A. I(1;-2;2), I(5;2;10)

B. I(1;-2;2), I(0;-3;0)

C. I(5;2;10), I(0;-3;0)

D. I(1;-2;2), I(-1;2;-2)

Câu 41:

Biết rằng $\int_{0}^{1} x c o s 2 x d x =$ $\frac{1}{4} (a \sin 2 + b \cos 2 + c)$ , với $a, b, c \in Z$ . Mệnh đề nào sau đây là đúng?

A. a+b+c=1

B. a-b+c=0

C. a+2b+c=1

D. 2a+b+c=-1

Câu 42:

Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng $\sqrt{3}$ a. Thể tích khối chóp S.ABCD bằng

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $4 a^{3} \sqrt{3}$

C. $a^{3} \sqrt{3}$

D. $\frac{a^{3} 4 \sqrt{3}}{3}$

Câu 43:

Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = \sqrt{x}$ ,y=0 và x=4 quanh trục Ox. Đường thẳng x=a (0<a<4) cắt đồ thị hàm số $y = \sqrt{x}$ tại M (hình vẽ bên). Gọi $V_{1}$ là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2 $V_{1}$ . Khi đó

A. a = $2 \sqrt{2}$

B. a = $\frac{5}{2}$

C. a = 2

D. a = 3

Câu 44:

Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:

A. $m \leq - 1$ hoặc $m \geq 3$

B. $m \leq - 3$ hoặc $m \geq 1$

C. m = -1 hoặc m = 3

D. $1 \leq m \leq 3$

Câu 45:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng $(α) : x = 1,$ $(β) : y = - 1,$ $(γ) : z = 1$ . Bán kính của mặt cầu (S) bằng

A. $\sqrt{33}$

B. 1

C. $3 \sqrt{2}$

D. 3

Câu 46:

Cho lăng trụ đứng ABC.A’B’C’ có AB = AC = a, $B C = a \sqrt{3}$ . Cạnh bên AA' = 2a. Bán kính mặt cầu ngoại tiếp tứ diện AB’C’C bằng

A. a

B. $a \sqrt{5}$

C. $a \sqrt{3}$

D. $a \sqrt{2}$

Câu 47:

Cho các số thực x, y thỏa mãn $x + y = 2 (\sqrt{x - 3} + \sqrt{y + 3})$ . Giá trị nhỏ nhất của biểu thức $P = 4 (x^{2} + y^{2}) + 15 x y$ là:

A. min⁡P = -83

B. min⁡P = -63

C. min⁡P = -80

D. min⁡P = -91

Câu 48:

Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm Trái đất nóng lên. Theo OECD (Tổ chức Hợp tác và Phát triển kinh tế thế giới), khi nhiệt độ Trái đất tăng lên thì tổng giá trị kinh tế toàn cầu giảm.

Người ta ước tính rằng, khi nhiệt độ Trái đất tăng thêm $2 °$ C thì tổng giá trị kinh tế toàn cầu giảm 3%; còn khi nhiệt độ Trái đất tăng thêm $5 °$ C thì tổng giá trị kinh tế toàn cầu giảm 10%. Biết rằng, nếu nhiệt độ Trái đất tăng thêm $t °$ C. Tổng giá trị kinh tế toàn cầu giảm f(t)% thì f(t) = $k . a^{t}$ , trong đó k, a là các hằng số dương.

Khi nhiệt độ Trái đất tăng thêm bao nhiêu $° C$ thì tổng giá trị kinh tế toàn cầu giảm đến 20%

A. 8,4 $° C$

B. 9,3 $° C$

C. 7,6 $° C$

D. 6,7 $° C$

Câu 49:

Cho các số phức z, w thỏa mãn |z+2-2i|=|z-4i|, w=iz+1. Giá trị nhỏ nhất của |w| là

A. $\frac{\sqrt{2}}{2}$

B. 2

C. $\frac{3 \sqrt{2}}{2}$

D. 2 $\sqrt{2}$

Câu 50:

Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ Oxy là $16 y^{2} = x^{2} (25 - x^{2})$ như hình vẽ bên. Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều dài 1 mét.

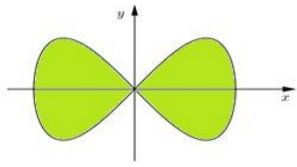
A. S = $\frac{125}{6}$ ( $m^{2}$ )

B. S = $\frac{125}{4}$ ( $m^{2}$ )

C. S = $\frac{250}{3}$ ( $m^{2}$ )

D. S = $\frac{125}{3}$ ( $m^{2}$ )

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 16)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 16)

CHỌN BỘ SÁCH BẠN MUỐN XEM