Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 18)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị là:
A. 2
B. 3
C. 4
D. 1
Đồ thị trong hình bên là của hàm số nào sau đây:
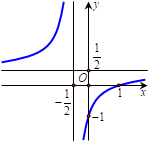
A. y =
B. y =
C. y =
D. y =
Rút gọn biểu thức: B = :
A. tana
B.
C.
D. tan2a
Cho hàm số . Tìm mệnh đề sai.
A. thì hàm số có hai điểm cực trị.
B. Hàm số luôn có cực đại và cực tiểu.
C. thì hàm số có cực đại và cực tiểu.
D. thì hàm số có cực trị.
Tìm m để hàm số có hai điểm cực đại và một điểm cực tiểu.
A. -3 < m < 0.
B. 0 < m < 3.
C. m < -3
D. 3 < m.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
A. min y = ; max y = 96
B. min y = ; max y = 6
C. min y = ; max y = 96
D. min y = 2; max y = 6
Hàm số nghịch biến trên khoảng
A. (0;1).
B. .
C. .
D. (1;2).
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số là
A. 2-.
B. 2.
C. 2+.
D. 1.
Biết đồ thị có tiệm cận đứng là x=1 và tiệm cận ngang là y=0. Tính a+2b.
A. 6.
B. 7.
C. 8.
D. 10.
Tìm m để Bất phương trình luôn đúng ?
A.
B.
C.
D.
2 cos^3x=sin3 xphương đã cho có nghiệm hoặc vậy A là:
A. 2
B. 3
C. 4
D. -2
Phương trình có nghiệm dạng a+. Khi đó a+b bằng:
A. 6
B. 4
C. 8
D. 10
Tập xác định của hàm số là:
A. .
B.
C. (;+∞).
D. .
Tích tất cả các nghiệm của phương trình bằng:
A. .
B. 2.
C. -1
D. 1.
Tập nghiệm của bất phương trình là:
A. .
B. .
C.
D. (1;2).
Cho hàm số . Tập nghiệm của bất phương trình là
A. .
B. .
C. .
D. .
Tìm tất cả các giá trị của m để hàm số đồng biến trên [1,2].
A. .
B. .
C. .
D. m > -8.
Ngân hàng A vừa qua đã thay đổi liên tục lãi suất tiền gửi tiết kiệm. Bác Khải gửi số tiền tiết kiệm ban đầu là 30 triệu đồng với lãi suất 0,8%/ tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2%/ tháng, trong nửa năm tiếp theo và bác Khải đã tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 0,9%/ tháng, bác Khải tiếp tục gửi thêm một số tháng tròn nữa, khi rút tiền bác Khải được cả vốn lẫn lãi là 35.956.304,69 đồng (chưa làm tròn). Hỏi bác Khải đã gửi tiết kiệm trong bao nhiêu tháng.
A. 13 tháng
B. 15 tháng
C. 17 tháng
D. 19 tháng
Tìm mệnh đề sai trong các mệnh đề sau?
A. Hàm số y=2^(3-x) nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số đạt cực đại tại x=0.
D. Giá trị nhỏ nhất của hàm số bằng 4.
Cho hàm số .
Tính giá trị biểu thức A = ?
A. 50
B. 49
C.
D.
Một nguồn âm đẳng hướng đặt tại điểm O có công suất truyền âm không đổi. Mức cường độ âm tại điểm M cách O một khoảng R được tính bởi công thức log (Ben) với k là hằng số. Biết điểm thuộc đoạn thẳng AB và mức cường độ âm tại A và B lần lượt là (Ben) và (Ben). Tính mức cường độ âm tại trung điểm AB (làm tròn đến 2 chữ số sau dấu phẩy).
A. 3,59 (Ben).
B. 3,06 (Ben).
C. 3,69 (Ben).
D. 4 (Ben).
Một ôtô đang chạy đều với vận tốc 15 m/s thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ôtô chuyển động chậm dần đều với gia tốc -a . Biết ôtô chuyển động thêm được 20m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây.
A. (3;4).
B. (4;5).
C. (5;6).
D. (6;7).
An và Bình chơi một trò chơi. An để một sấp tấm bìa cứng nhỏ trên có ghi tương ứng các số từ 1 đến 30. Luật chơi như sau: Khi đến lượt, người chơi sẽ rút ngẫu nhiên 3 tấm bìa trong sấp và tính tổng các số ghi trên mỗi tấm bìa, trò chơi kết thúc khi có người thắng là người rút trúng 3 tấm bìa trên đó tổng các số chia hết cho 3. Lưu ý rằng không được để lại các tấm bìa đã rút vào sấp bài. Nếu Bình bốc trước, xác suất để Bình thắng ngay trong lượt đầu là:
A.
B.
C.
D.
An và Bình chơi một trò chơi. An để một sấp tấm bìa cứng nhỏ trên có ghi tương ứng các số từ 1 đến 30. Luật chơi như sau: Khi đến lượt, người chơi sẽ rút ngẫu nhiên 3 tấm bìa trong sấp và tính tổng các số ghi trên mỗi tấm bìa, trò chơi kết thúc khi có người thắng là người rút trúng 3 tấm bìa trên đó tổng các số chia hết cho 3. Lưu ý rằng không được để lại các tấm bìa đã rút vào sấp bài. Nếu Bình bốc trước, xác suất để Bình thắng ngay trong lượt đầu là:
A.
B.
C.
D.
Biết hàm số là một nguyên hàm của hàm số . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Cho n là số nguyên dương thoả mãn . Tìm hệ số số hạng chứa trong khai triển nhị trức Niu- tơn của
A.
B.
C.
D.
Có bao nhiêu số sao cho
A.
B.
C.
D.
Tính tổng: S =
A.
B.
C.
D.
Cho số phức z thỏa mãn |z-2-3i|=1. Giá trị lớn nhất của |+1+i| là
A. +2.
B. 4.
C. 6.
D. +1.
Cho phương trình = 0
Các phát biểu :
(1) Phương trình trên vô nghiệm vơi mọi m
(2) Khi m = 1 phương trình trên có nghiệm
(3) Không tồn tại m để phương trình trên vô nghiệm
Chọn đáp án đúng:
A. (1) đúng
B. (2),(3) Đúng
C. A, B đều đúng
D. Tất cả đều sai.
Cho hàm số y=x.sinx. Tính :
A. 0
B. 1
C. 2
D. 3
Biết phương trình có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Có bao nhiêu số phức z thỏa mãn: |z-i|= và là số thuần ảo:
A. 3
B. 1
C. 4
D. 2
Cho A,B,C là các điểm biểu diễn các số phức thỏa mãn . Tìm phát biểu sai:
A. Tam giác ABC đều.
B. Tam giác ABC có trọng tâm là O(0;0).
C. Tam giác ABC có tâm đường tròn ngoại tiếp là O(0;0).
D.
Một chiếc xô hình nón cụt đựng hóa chất ở phòng thí nghiệm có chiều cao 20cm, đường kính hai đáy lần lượt là 10cm và 20cm. Cô giáo giao cho bạn An sơn mặt ngoài của xô (trừ đáy). Tính diện tích bạn An phải sơn (làm tròn đến hai chữ số sau dấu phẩy).
A. 1942,97.
B. 561,25.
C. 971,48.
D. 2107,44.
Xét các hình chóp S.ABC có SA=SB=SC=AB=BC=a. Giá trị lớn nhất của thể tích hình chóp S.ABC bằng:
A.
B.
C.
D.
Cho khối chóp S.ABCD có thể tích bằng . Mặt bên SAB là tam giác đều cạnh a và đáy ABCD là hình bình hành. Tính theo a khoảng cách giữa SA và CD.
A.
B.
C.
D.
Người ta muốn xây một cái bể chứa nước dạng khối hộp chữ nhật không nắp có thể tích . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/. Nếu biết xác định kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất, chi phí thấp nhất đó là
A. 75 triệu đồng
B. 70 triệu đồng
C. 80 triệu đồng
D. 85 triệu đồng
Khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a. SA=SB=SC=a, Cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:
A.
B.
C.
D.
Cho khối nón đỉnh O, trục OI. Măt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
A.
B.
C.
D.
Cho hình trụ có trục OO', thiết diện qua trục là một hình vuông cạnh 2a. Mặt phẳng (P) song song với trục và cách trục một khoảng . Tính diện tích thiết diện của trụ cắt bởi (P).
A.
B.
C.
D.
Một cốc nước hình trụ có chiều cao 9cm, đường kính 6cm. Mặt đáy phẳng và dày 1cm, thành cốc dày 0,2cm. Đổ vào cốc 120ml nước sau đó thả vào cốc 5 viên bi có đường kính 2cm. Hỏi mặt nước trong cốc cách mép cốc bao nhiêu cm. (Làm tròn đến hai chữ số sau dấu phẩy).
A. 3,67cm.
B. 2,67cm.
C. 3,28cm.
D. 2,28cm.
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;2;1), B(3;0;-1) và mặt phẳng (P):x+y-z-1=0. Gọi M và N lần lượt là hình chiếu của A và B trên mặt phẳng (P). Tính độ dài đoạn MN.
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;2;1) và mặt phẳng (P):x+2y-2z-1=0. Gọi B là điểm đối xứng với A qua (P). Độ dài đoạn thẳng AB là
A. 2
B.
C.
D. 4
Trong không gian với hệ tọa độ Oxyz cho các vectơ =(1;2;1), =(-2;3;4), =(0;1;2), =(4;2;0). Biết =x.+y.+z.. Tổng x+y+z là
A. 2
B. 3
C. 5
D. 4
Bên trong hình vuông cạnh a, dựng hình sao cho bốn cạnh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình). Tính thể tích của khối tròn xoay sinh ra khi quay hình sao đó quay trục xy.

A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và đường thẳng d có phương trình . Mặt phẳng chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
A. .
B. .
C. .
D. .
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):2x+y-z-1=0 và (Q):x-2y+z-5=0. Khi đó, giao tuyến của (P) và (Q) có một vectơ chỉ phương là:
A. = (1;3;5).
B. = (-1;3;-5).
C. = (2;1;-1).
D. = (1;-2;1).
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M lần lượt cắt các tia Ox,Oy,Oz tại A,B,C khác O. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC.
A. 54.
B. 6.
C. 9.
D. 18.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt cầu (S): = 2. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M,N là tiếp điểm. Tính độ dài đoạn thẳng MN.
A.
B.
C.
D. 4