Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 19)

Câu 1:

Cho góc $α$ thỏa mãn $5 \sin 2 α - 6 \cos α = 0$ và $0 < α < \frac{π}{2}$ .

Tính giá trị của biểu thức: A = $\cos (\frac{π}{2} - α) + \sin (2015 π - α)$ $- c o t (2016 π + α) .$

A. $\frac{- 2}{15}$

B. $\frac{4}{15}$

C. $\frac{1}{15}$

D. $\frac{- 3}{5}$

Câu 2:

Giả sử $\int_{1}^{2} \frac{4 \ln x + 1}{x} d x$ $= a l n^{2} 2 + b l n 2$ , với a, b là các số hữu tỉ. Khi đó tổng 4a+b bằng

A. 3

B. 5

C. 7

D. 9

Câu 3:

Diện tích hình phẳng được giới hạn bởi các đồ thị hàm số $y = x^{2}$ và y=x là:

A. $\frac{1}{2}$ (đvdt)

B. $\frac{1}{3}$ (đvdt)

C. $\frac{1}{4}$ (đvdt)

D. $\frac{1}{6}$ (đvdt)

Câu 4:

Cho tan a = 2. Tính giá trị biểu thức: E= $\frac{8 \cos^{3} a - 2 \sin^{3} a + \cos a}{2 c o s a - s i n^{3} a}$

A. $\frac{- 3}{2}$

B. 2

C. 4

D. $\frac{5}{2}$

Câu 5:

Người ta thiết kế một bể cá bằng kính không có nắp với thể tích 72 $d m^{3}$ và có chiều cao bằng 3 dm. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bể dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.

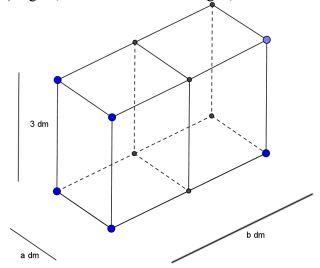
A. a= $\sqrt{24}$ , b= $\sqrt{21}$

B. a=3,b=8

C. a=3 $\sqrt{2}$ , b=4 $\sqrt{2}$

D. a=4,b=6

Câu 6:

Tìm k để GTNN của hàm số $y = \frac{k \sin x + 1}{\cos x + 2}$ lớn hơn -1?

A. $| k | \leq \sqrt{2}$

B. $| k | \leq 2 \sqrt{3}$

C. $| k | \leq 2 \sqrt{2}$

D. $| k | \leq \sqrt{3}$

Câu 7:

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a;AD=2a và AA'=3a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ACB’D’.

A. $\frac{a \sqrt{3}}{2}$

B. $\frac{a \sqrt{14}}{2}$

C. $\frac{a \sqrt{6}}{2}$

D. $\frac{a \sqrt{3}}{4}$

Câu 8:

Tìm tập xác định của hàm số $y = \tan (2 x + \frac{π}{6})$

A. $x \neq \frac{π}{6} + k \frac{π}{2}$

B. R

C. $x \neq \frac{π}{6} + k π$

D. $x \neq \frac{π}{12} + k \frac{π}{2}$

Câu 9:

Tìm chu kỳ của những hàm số sau đây: y = tan3x+cot2x

A. $\frac{2 π}{3}$

B. $\frac{π}{3}$

C. $π$

D. $2 π$

Câu 10:

Tổng các nghiệm của phương trình $s i n^{2} 2 x + s i n^{2} 4 x = \frac{3}{2}$ trên đoạn [0, $\frac{π}{2}$ ] là:

A. $\frac{7 π}{4}$

B. $\frac{3 π}{4}$

C. $π$

D. $\frac{5 π}{4}$

Câu 11:

Đội bóng MU tiến hành tuyển chọn những tài năng nhí để đào tạo. Sau một quá trình đã chọn được 16 ứng viên, trong đó có 4 ứng viên 10 tuổi, 5 ứng viên 11 tuổi và 7 ứng viên 12 tuổi. Các ứng viên cùng độ tuổi sẽ có những đặc điểm có thể coi giống nhau. Trong dự định tuyển chọn có quyết định rằng chỉ tuyển 4 ứng viên, trong đó có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi. Trong giờ nghỉ của buổi tuyển chọn, huấn luyện viên có thử lựa chọn ngẫu nhiên 4 ứng viên, xác suất 4 ứng viên đó thỏa mãn dự định tuyển chọn là:

A. $\frac{37}{91}$

B. $\frac{54}{91}$

C. $\frac{33}{91}$

D. $\frac{58}{91}$

Câu 12:

Tìm m để phương trình m ln⁡(1-x)-ln⁡x = m có nghiệm $x \in (0; 1)$

A. $m \in (0; + \infty)$

B. $m \in (1; e)$

C. $m \in (- \infty; 0)$

D. $m \in (- \infty; - 1)$

Câu 13:

Số tiệm cận ngang của hàm số $y = \frac{x}{\sqrt{x^{2} + 1}}$ là:

A. 0

B. 1

C. 2

D. 3

Câu 14:

Tập nghiệm của phương trình $l o g_{3} (l o g_{\frac{1}{2}} x) < 1$ là

A. (0;1)

B. ( $\frac{1}{8}$ ;1)

C. (1;8)

D. ( $\frac{1}{8}$ ;3)

Câu 15:

Tìm hệ số của số hạng chứa $x^{10}$ trong khai triển biểu thức ${(x^{3} - \frac{1}{x^{2}})}^{n}$ , biết n là số tự nhiên thỏa mãn $C_{n}^{4} = 13 C_{n}^{n - 2}$

A. 6435

B. 5005

C. -5005

D. -6435

Câu 16:

Trong số các số phức z thỏa mãn điều kiện |z-4+3i|=3, gọi $z_{0}$ là số phức có mô đun lớn nhất. Khi đó | $z_{0}$ | là:

A. 3

B. 4

C. 5

D. 8

Câu 17:

Biết $F (x) = (a x + b) . e^{x}$ là nguyên hàm của hàm số $y = (2 x + 3) . e^{x}$ . Khi đó a+b là

A. 2

B. 3

C. 4

D. 5

Câu 18:

Trong không gian với hệ trục tọa độ Oxyz viết phương trình mặt phẳng (P) song song và cách đều đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}$ và $d_{2} : \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$

A. (P):2x-2z+1=0

B. (P):2y-2z+1=0

C. (P):2x-2y+1=0

D. (P):2y-2z-1=0

Câu 19:

Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(1;2;-1);C(3;-4;1),B'(2;-1;3) và D'(0;3;5). Giả sử tọa độ D(x;y;z) thì giá trị của x+2y-3z là kết quả nào sau đây

A. 1

B. 0

C. 2

D. 3

Câu 20:

Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y-z+3=0 và đường thẳng (d): $\frac{x - 1}{1} = \frac{y + 3}{2} = \frac{z}{2}$ . Gọi A là giao điểm của (d) và (P); gọi M là điểm thuộc (d) thỏa mãn điều kiện MA = 2. Tính khoảng cách từ M đến mặt phẳng (P)?

A. $\frac{4}{9}$

B. $\frac{8}{3}$

C. $\frac{8}{9}$

D. $\frac{2}{9}$

Câu 21:

Dân số thế giới được ước tính theo công thức $S = A . e^{n . i}$ trong đó A là dân số của năm lấy làm mốc, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm. Theo thống kê dân số thế giới tính đến tháng 01/2017, dân số Việt Nam có 94,970 người và có tỉ lệ tăng dân số là 1,03%. Nếu tỉ lệ tăng dân số không đổi thì đến năm 2020 dân số nước ta có bao nhiêu triệu người, chọn đáp án gần nhất.

A. 98 triệu người

B. 100 triệu người

C. 100 triệu người

D. 104 triệu người

Câu 22:

Từ khai triển biểu thức ${(x - 1)}^{100} = a_{0} x^{100}$ $+ a_{1} x^{99} + . . . + a_{98} x^{2}$ $+ a_{99} x + a_{100} .$ Tính tổng S = $100 a_{0} . 2^{100} + 99 a_{1} . 2^{99}$ $+ . . . + 2 a_{98} 2^{2} + 1 a_{99} 2^{1} + 1$

A. 201

B. 202

C. 203

D. 204

Câu 23:

Cho $a = \log_{2} 20$ . Tính $\log_{20} 5$ theo a

A. $\frac{5 a}{2}$

B. $\frac{a + 1}{a}$

C. $\frac{a - 2}{a}$

D. $\frac{a + 1}{a - 2}$

Câu 24:

Biết rằng đồ thị $y = x^{3} + 3 x^{2}$ có dạng như sau:

Hỏi đồ thị hàm số $y = | x^{3} + 3 x^{2} |$ có bao nhiêu điểm cực trị?

A. 0

B.1

C. 2

D. 3

Câu 25:

Gọi M mà m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y = \frac{\sqrt{1 - x} - 2 x^{2}}{\sqrt{x} + 1}$ . Khi đó giá trị của M-m là:

A. -2

B. -1

C. 1

D. 2

Câu 26:

Tìm tập nghiệm của bất phương trình $3^{\sqrt{2 x} + 1} - 3^{x + 1} \leq x^{2} - 2 x$ là:

A. $(0; + \infty)$

B. $[0; 2]$

C. $[2; + \infty)$

D. $[2; + \infty) \cup \{0\}$

Câu 27:

Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc với đáy, cạnh bên SB tạo với đáy một góc $60 °$ , đáy ABC là tam giác vuông cân tại B với BA=BC=a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích khối đa diện AMNBC?

A. $\frac{a^{3} \sqrt{3}}{4}$

B. $\frac{a^{3} \sqrt{3}}{6}$

C. $\frac{a^{3} \sqrt{3}}{24}$

D. $\frac{a^{3} \sqrt{3}}{8}$

Câu 28:

Với giá trị nào của m thì x=1 là điểm cực tiểu của hàm số y = $\frac{1}{3} x^{3} + m x^{2} + (m^{2} + m + 1) x$

A. $m \in \{- 2; - 1\}$

B. m = -2

C. m = -1

D. Không có m

Câu 29:

Cho số phức z=a+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận $z$ làm nghiệm với mọi a, b là:

A. $z^{2} = a^{2} - b^{2} + 2 a b i$

B. $z^{2} = a^{2} + b^{2}$

C. $z^{2} - 2 a z + a^{2} + b^{2} = 0$

D. $z^{2} + 2 a z + a^{2} - b^{2} = 0$

Câu 30:

Biết đồ thị hàm số y = $a x^{3} + b x^{2} + c x + d$ có 2 điểm cực trị là (-1;18) và (3;-16). Tính a+b+c+d

A. 0

B. 1

C. 2

D. 3

Câu 31:

Biết đồ thị hàm số $y = x^{4} - 4 x^{2} + 3$ có bảng biến thiên như sau:

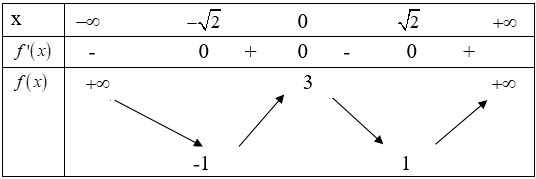
Tìm m để phương trình $| x^{4} - 4 x^{2} + 3 | = m$ có đúng 4 nghiệm phân biệt

A. 1 < m < 3

B. m > 3

C. m = 0

D. $m \in (1; 3) \cup \{0\}$

Câu 32:

Cho cấp số nhân $(u_{n})$ có $S_{2} = 4; S_{3} = 13$ . Khi đó $S_{5}$ bằng:

A. 121 hoặc $\frac{35}{16}$

B. 121 hoặc $\frac{181}{16}$

C. 144 hoặc $\frac{185}{16}$

D. 141 hoặc $\frac{183}{16}$

Câu 33:

Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;2;1); B(3;2;3) , có tâm thuộc mặt phẳng (P):x-y-3=0, đồng thời có bán kính nhỏ nhất, hãy tính bán kính R thuộc mặt cầu (S)?

A. 1

B. $\sqrt{2}$

C. 2

D. $2 \sqrt{2}$

Câu 34:

Giới hạn $\underset{x \to + \infty}{l i m} \frac{{(x - 1)}^{2} (2 x^{3} + 3 x)}{4 x - x^{5}}$ bằng $\frac{a}{b}$ (phân số tối giản). giá trị của $A = a^{2} - b^{2}$ là:

A. -3

B. -2

C. 2

D. 3

Câu 35:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-1;1); B(2;1;-2), C(0;0;1) . Gọi H(x;y;z) là trực tâm của tam giác ABC thì giá trị của x+y+z là kết quả nào dưới đây?

A. 1

B. $\frac{1}{3}$

C. 2

D. 3

Câu 36:

Tính đạo hàm của các hàm số y = $\frac{{(x + 1)}^{2}}{{(x - 1)}^{3}} .$

A. y' = $2 (x + 1) (x - 1)^{- 3}$ $- 3 (x + 1)^{2} (x - 1)^{2} .$

B. y' = $2 (x + 1) (x - 1)^{3}$ $- 3 (x + 1)^{2} (x - 1)^{- 2} .$

C. y' = $2 {(x + 1)}^{2} (x - 1)^{- 3}$ $- 3 (x + 1)^{2} (x - 1)^{- 4} .$

D. y' = $2 (x + 1) (x - 1)^{- 3}$ $- 3 (x + 1)^{2} (x - 1)^{- 2} .$

Câu 37:

Cho z là số phức thỏa mãn z+ $\frac{1}{z}$ =1. Tính giá trị của $z^{2017} + \frac{1}{z^{2017}}$

A. -2

B. -1

C. 1

D. 2

Câu 38:

Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với A(-1;2;1), B(0;0;-2); C(1;0;1); D(2;1;-1). Tính thể tích tứ diện ABCD?

A. $\frac{1}{3}$

B. $\frac{2}{3}$

C. $\frac{4}{3}$

D. $\frac{8}{3}$

Câu 39:

Cho $x = l o g_{6} 5$ ; $y = l o g_{2} 3$ ; $z = l o g_{4} 10$ ; $t = l o g_{7} 5$ . Chọn thứ tự đúng

A. z>x>t>y

B. z>y>t>x

C. y>z>x>t

D. z>y>x>t

Câu 40:

Có bao nhiêu số nguyên dương n sao cho $n . l n n - \int_{1}^{n} l n x d x$ có giá trị không vượt quá 2017

A. 2017

B. 2018

C. 4034

D. 4036

Câu 41:

Cho hình trụ có hai đường tròn đáy lần lượt là (O); (O’). Biết thể tích khối nón có đỉnh là O và đáy là hình tròn (O’) là $a^{3}$ , tính thể tích khối trụ đã cho ?

A. 2 $a^{3}$

B. 4 $a^{3}$

C. 6 $a^{3}$

D. 3 $a^{3}$

Câu 42:

Cho hàm số $f (x) = \{\begin{cases} \frac{3 - \sqrt{4 - x}}{4} k h i x \neq 0 \\ \frac{1}{4} k h i x = 0 \end{cases}$ Khi đó f'(0) là kết quả nào sau đây?

A. $\frac{1}{4}$

B. $\frac{1}{16}$

C. $\frac{1}{32}$

D. Không tồn tại

Câu 43:

Với $a, b, c > 0; a \neq 1; α \neq 0$ bất kì. Tìm mệnh đề sai

A. $l o g_{a} (b c) = l o g_{a} b + l o g_{a} c$

B. $l o g_{a} \frac{b}{c} = l o g_{a} b - l o g_{a} c$

C. $l o g_{α^{a}} b = α l o g_{a} b$

D. $l o g_{a} b . l o g_{c} a = l o g_{c} b$

Câu 44:

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(3;0;0),B(0;2;0);C(0;0;6) và D(1;1;1). Gọi là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A, B, C đến $Δ$ là lớn nhất đi qua điểm nào trong các điểm dưới đây?

A. M(-1;-2;1)

B. (5;7;3)

C. (3;4;3)

D. (7;13;5)

Câu 45:

Trên mặt phẳng phức, cho điểm A biểu diễn số phức 3-2i , điểm B biểu diễn số phức -1+6i. Gọi M là trung điểm của AB. Khi đó điểm M biểu diễn số phức nào trong các số phức sau:

A. 1-2i

B. 2-4i

C. 2+4i

D. 1+2i

Câu 46:

Tại một thời điểm t trước lúc đỗ xe ở trạm dừng nghỉ, ba xe đang chuyển động đều với vận tốc lần lượt là 60km/h; 50km/h; 40km/h. Xe thứ nhật đi thêm 4 phút thì bắt đầu chuyển động chậm dần đều và dừng hẳn ở trạm tại phút thứ 8; xe thứ 2 đi thêm 4 phút thì bắt đầu chuyển động chậm dần đều và dừng hẳn ở trạm tại phút thứ 13; xe thứ 3 đi thêm 8 phút và cũng bắt đầu chuyển động chậm dần đều và dừng hẳn ở trạm tại phút thứ 12. Đồ thị biểu diễn vận tốc ba xe theo thời gian như sau: (đơn vị trục tung ×10km/h , đơn vị trục tung là phút)

Giả sử tại thời điểm t trên, ba xe đang cách trạm lần lượt là $d_{1}; d_{2}; d_{3}$ .

So sánh khoảng cách này.

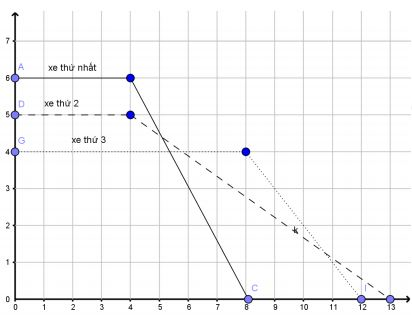
A. $d_{1} < d_{2} < d_{3}$

B. $d_{2} < d_{3} < d_{1}$

C. $d_{3} < d_{1} < d_{2}$

D. $d_{1} < d_{3} < d_{2}$

Câu 47:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C với CA=CB=a;SA=a $\sqrt{3}$ ; SB=a $\sqrt{5}$ và SC=a $\sqrt{2}$ . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC?

A. $\frac{a \sqrt{11}}{6}$

B. $\frac{a \sqrt{11}}{2}$

C. $\frac{a \sqrt{11}}{3}$

D. $\frac{a \sqrt{11}}{4}$

Câu 48:

Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN $⊥$ PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN=60cm và thể tích của khối tứ diện MNPQ bằng 30 $d m^{3}$ . Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)

A. 101,3 $d m^{3}$

B. 121,3 $d m^{3}$

C. 111,4 $d m^{3}$

D. 141,3 $d m^{3}$

Câu 49:

Với a,b > 0 bất kì. Cho biểu thức $\frac{a^{\frac{2}{3}} \sqrt{b} + b^{\frac{2}{3}} \sqrt{a}}{\sqrt[6]{a} + \sqrt[6]{b}}$ . Tìm mệnh đề đúng

A. P = $\sqrt{a b}$

B. P = $\sqrt[3]{a b}$

C. P = $\sqrt[6]{a b}$

D. P = ab

Câu 50:

Xét các hình chóp S.ABC thỏa mãn SA=a;SB=2a;SC=3a với a là hằng số cho trước. Tìm giá trị lớn nhất của thể tích khối chóp S.ABC?

A. 6 $a^{3}$

B. 2 $a^{3}$

C. $a^{3}$

D. 3 $a^{3}$

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 19)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 19)

CHỌN BỘ SÁCH BẠN MUỐN XEM