Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 3)

Câu 1:

Một phòng học có 15 bộ bàn ghế, xếp chỗ ngồi cho 30 học sinh, mỗi bàn ghế 2 học sinh. Tìm xác suất để hai học sinh A, B chỉ định trước ngồi cùng một bàn.

A. $\frac{1}{90}$

B. $\frac{1}{29}$

C. $\frac{96}{270725}$

D. $\frac{13536}{270725}$

Câu 2:

Hệ số của $x^{5}$ trong khai triển $x (1 - 2 x)^{5} + x^{2} (1 + 3 x)^{10}$ là:

A. 61204

B. 3160

C. 3320

D. 61268

Câu 3:

Có bao nhiêu phép tịnh tiến biến đồ thị của hàm số y = s⁡inx thành chính nó?

A. 0

B. 1

C. 2

D. Vô số

Câu 4:

Giá trị nhỏ nhất của hàm số $y = l n (x^{2} - 2 x + 1) - x$ trên đoạn [2;4] là:

A. 2ln2 - 3

B. 2ln2 - 4

C. - 2

D. - 3

Câu 5:

Tìm giá trị lớn nhất của hàm số $f (x) = \sin (π | \sin x |) .$

A. 1

B. $\frac{1}{4}$

C. $\frac{1}{2}$

D. 0

Câu 6:

Cho hàm số y=f(x) liên tục, đồng biến trên đoạn [a;b]. Khẳng định nào sau đây đúng?

A. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng (a; b)

B. Hàm số đã cho có cực trị trên đoạn [a;b]

C. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [a;b]

D. Phương trình f(x) = 0 có nghiệm duy nhất thuộc đoạn [a;b]

Câu 7:

Trong một hình đa diện lồi, mỗi cạnh là cạnh chung của tất cả bao nhiêu mặt?

A. 5

B. 3

C. 4

D. 2

Câu 8:

Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây đúng?

A. Hàm số có hai điểm cực trị

B. Hàm số nghịch biến trên mỗi khoảng xác định

C. Hàm số có một điểm cực trị

D. Giá trị lớn nhất của hàm số là 3

Câu 9:

Tìm m để hàm số $y = x^{3} + 2 x^{2} - m x + 1$ đồng biến trên R.

A. $m < - \frac{4}{3}$

B. $m \leq - \frac{4}{3}$

C. $m \geq - \frac{4}{3}$

D. $m > - \frac{4}{3}$

Câu 10:

Cho tích phân $I = \int_{0}^{π} x^{2} \cos x d x$ và $u = x^{2}, d v = \cos d x$ . Khẳng định nào sau đây đúng?

A. $I = x^{2} \sin x |_{0}^{π} - 2 \int_{0}^{π} x . \sin x d x$

B. $I = x^{2} \sin x |_{0}^{π} - \int_{0}^{π} x . \sin x d x$

C. $I = x^{2} \sin x |_{0}^{π} + \int_{0}^{π} x . \sin x d x$

D. $I = x^{2} \sin x |_{0}^{π} + 2 \int_{0}^{π} x . \sin x d x$

Câu 11:

Tìm tất cả các đường tiệm cận của đồ thị hàm số $y = \frac{x - \sqrt{x^{2} - 4}}{x^{2} - 4 x + 3}$ là

A. y = 1 và x = 3

B. y = 0, y = 1 và x = 3

C. y = 0 và x = 3, x = 1

D. y = 0 và x = 3

Câu 12:

Cho hàm số y=f(x) thỏa mãn $f' (x) = (x + 1) e^{x}$ và $\int f (x) d x = (a x + b) e^{x} + c$ với a, b, c là các hằng số. Khi đó:

A. a + b = 0

B. a + b = 3

C. a + b = 2

D. a + b = 1

Câu 13:

Số giao điểm của đồ thị hàm số $y = x^{3} - 3 x^{2} + 3 x - 1$ và $y = x^{2} - x - 1$ là:

A. 3

B. 1

C. 0

D. 2

Câu 14:

Cho hàm số y = f(x) = $\frac{a x + b}{c x + d}$ có đồ thị như hình vẽ bên. Tất cả các giá trị của m để phương trình |f(x)| = m có 2 nghiệm phân biệt là:

$A . m \geq 2 v à m \leq 1$

$B . 0 < m < 1 v à m > 1$

$C . m > 2 v à m < 1$

$D . 0 < m < 1$

Câu 15:

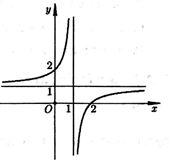
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-1;3] và có đổ thị như hình vẽ bên. Tiếp tuyến của đổ thị hàm số tại điểm x = 2 có hệ số góc bằng?

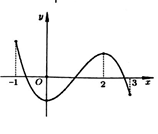
A. -1

B. 1

C. 0

D. 2

Câu 16:

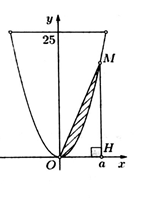
Ông B có một khu vườn giới hạn bởi một đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxỵ như hình vẽ bên thì parabol có phương trình $y = x^{2}$ và đường thẳng là y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua O và điểm M trên parabol để trồng một loại hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ bằng $\frac{9}{2}$ .

A. $O M = 2 \sqrt{5}$

B. $O M = 15$

C. $O M = 10$

D. $O M = 3 \sqrt{10}$

Câu 17:

Cho hàm số y = f(x) có đổ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn hàm số được đưa ra trong các phương án A, B, C, D dưới đây. Tìm f(x)

$A . f (x) = e^{x}$

$B . f (x) = (\frac{3}{π})^{x}$

$C . f (x) = \ln x$

$D . f (x) = x^{\frac{e}{π}}$

Câu 18:

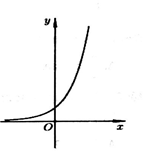
Cho hai số thực dương x, y bất kỳ. Khẳng định nào sau đây đúng?

A. $\log_{2} \frac{x^{2}}{y} = \frac{2 \log_{2} x}{\log_{2} y}$

B. $\log_{2} (x^{2} y) = 2 \log_{2} x + \log_{2} y$

C. $\log_{2} (x^{2} + y) = 2 \log_{2} x . \log_{2} y$

D. $\log_{2} (x^{2} y) = \log_{2} x + 2 \log_{2} y$

Câu 19:

Nghiệm của bất phương trình $\log_{2} (x + 1) + \log_{\frac{1}{2}} \sqrt{x + 1} \leq 0$ là:

$A . - 1 < x \leq 0$

$B . - 1 \leq x \leq 0$

$C . - 1 \leq x \leq 1$

$D . x \leq 0$

Câu 20:

Phương trình $1 + a + a^{2} + . . . + a^{x} = (1 + a) (1 + a^{2}) (1 + a^{4})$ với $0 < a \neq 1$ có bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 3

Câu 21:

Tất cả các giá trị của m để phương trình $e^{x} = m (x + 1)$ có nghiệm duy nhất là:

$A . m > 1$

$B . m < 0, m \geq 1$

$C . m < 0, m = 1$

$D . m < 1$

Câu 22:

Tính giá trị $S = 1 + 2^{2} \log_{\sqrt{2}} 2 + 3^{2} \log_{\sqrt[3]{2}} 2 + . . . + 2017^{2} \log_{\sqrt[2017]{2}} 2 .$

$A . S = 1008^{2} . 2017^{2}$

$B . S = 1007^{2} . 2017^{2}$

$C . S = 1009^{2} . 2017^{2}$

$D . S = 1010^{2} . 2017^{2}$

Câu 23:

Cho tứ diện ABCD có AB = 4a, CD = 6a, các cạnh còn lại đều bằng $a \sqrt{22}$ . Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.

A. $\frac{5 a}{2}$

B. 3a

C. $\frac{a \sqrt{85}}{3}$

D. $\frac{a \sqrt{79}}{3}$

Câu 24:

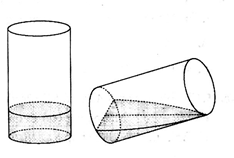
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MN $⊥$ PQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được khối đá có hình tứ diện MNPQ. Biết rằng MN = 60cm và thể tích khối tứ diện MNPQ bằng $30 d m^{3}$ Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).

$A . 101, 3 d m^{3}$

$B . 141, 3 d m^{3}$

$C . 121, 3 d m^{3}$

$D . 111, 4 d m^{3}$

Câu 25:

Cho hình nón đỉnh S. Xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của hình nón và có AB = BC = 10a, AC = 12a góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng $45 °$ . Tính thể tích khối nón đã cho.

$A . 9 π a^{3}$

$B . 27 π a^{3}$

$C . 3 π a^{3}$

$D . 12 π a^{3}$

Câu 26:

Cho z là một số phức tùy ý khác 0. Khẳng định nào sau đây sai?

A. $\frac{z}{z}$ là số ảo

B. $z - z$ là số ảo

C. $z . z$ là số thực

D. $z + z$ là số ảo

Câu 27:

Biết rằng phương trình $z^{2} + b z + c = 0 (b, c \in R)$ có một nghiệm phức là $z_{1} = 1 + 2 i$ . Khi đó:

A. b + c = 2

B. b + c = 3

C. b + c = 0

D. b + c = 7

Câu 28:

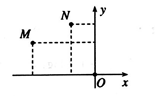
Gọi M và N lấn lượt là điểm biểu diễn của các số phức $z_{1}, z_{2}$ như hình vẽ bên. Khi đó khẳng định nào sau đây sai?

$A . | z_{1} - z_{2} | = M N$

$B . | z_{1} | = O M$

$C . | z_{2} | = O N$

$D . | z_{1} + z_{2} | = M N$

Câu 29:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 1}{1} = \frac{y - 2}{- 2} = \frac{z - 3}{1}$ và $d_{2} : \{\begin{cases} x = 1 + k t \\ y = t \\ z = - 1 + 2 t \end{cases}$ Tìm giá trị của k để $d_{1}$ cắt $d_{2}$ .

A. k = 0

B. k = 1

C. k = -1

D. $k = \frac{- 1}{2}$

Câu 30:

Trong không gian vỏi hệ tọa độ Oxỵz, cho đường thẳng $△ : \frac{x + 1}{2} = \frac{y - 2}{- 1} = \frac{z}{2} .$ Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(2; -3; 1) lên $△$

$A . H (- 3; - 1; - 2)$

$B . H (- 1; - 2; 0)$

$C . H (3; - 4; 4)$

$D . H (1; - 3; 2)$

Câu 31:

Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của tham số m để phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 m y + 6 z + 13 = 0$ là phương trình của mặt cầu.

$A . m > 0$

$B . m \neq 0$

$C . m \in R$

$D . m > 0$

Câu 32:

Trong không gian với hệ tọa độ Oxỵz, cho hai mặt phẳng (P): 2x + ay + 3z - 5 = 0 và (Q):4x - y - (a + 4)z + l = 0. Tìm a để (P) và (Q) vuông góc với nhau.

A. a = 1

B. a = 0

C. a = -1

D. $a = \frac{1}{3}$

Câu 33:

Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; 2;-3) và mặt phẳng(P):2x+2y-z+9=0. Đường thẳng d đi qua A và có véctơ chỉ phương $\overset{⇀}{u}$ =(3;4;-4) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc $90 °$ . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?

$A . H (- 2; - 1; 3)$

$B . I (- 1; - 2; 3)$

$C . K (3; 0; 15)$

$D . J (- 3; 2; 7)$

Câu 34:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y+z+6=0. Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.

$A . M (0; 0; 21)$

$B . M (0; 0; 3)$

$C . M (0; 0; 3), M (0; 0; - 15)$

$D . M (0; 0; - 15)$

Câu 35:

Cho hình chóp S.ABC có SC = 2a và SC $⊥$ (ABC). Đáy ABC là tam giác vuông cân tại B và có AB = $a \sqrt{l 2}$ . Mặt phẳng $(α)$ đi qua C và vuông góc với SA, $(α)$ cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.

A. $\frac{4 a^{3}}{9}$

B. $\frac{2 a^{3}}{3}$

C. $\frac{2 a^{3}}{9}$

D. $\frac{a^{3}}{3}$

Câu 36:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AA' = $a \sqrt{3}$ . Gọi I là giao điểm của AB’ và A’B. Cho biết khoảng cách từ I đến mặt phẳng (BCC'B')bằng $\frac{a \sqrt{3}}{2}$ . Tính thể tích khối lăng trụ ABC.A’B’C’.

A. $3 a^{3}$

B. $a^{3}$

$a^{3}$ . $\frac{3 a^{3}}{4}$

D. $\frac{a^{3}}{4}$

Câu 37:

Cho $I = \int_{1}^{2} x x \sqrt{4 - x^{2}} d x$ và $t = \sqrt{4 - x^{2}}$ . Khẳng định nào sau đây sai?

A. $\sqrt{3}$

B. $I = \frac{t^{2}}{2} |_{0}^{\sqrt{3}}$

C. $I = \int_{0}^{\sqrt{3}} t^{2} d t$

D. $I = \frac{t^{3}}{3} |_{0}^{\sqrt{3}}$

Câu 38:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đểu cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng mặt phẳng (SBC) tạo với mặt phảng đáy một góc $30 °$ .

A. $\frac{\sqrt{3} a^{3}}{2}$

B. $2 \sqrt{3} a^{3}$

C. $\frac{2 \sqrt{3} a^{3}}{3}$

C. $\frac{4 \sqrt{3} a^{3}}{3}$

Câu 39:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 2} = \frac{y}{- 1} = \frac{z - 2}{1}$ và hai điểm A(-1;3;1),B(0;2;-1). Tìm tọa độ điểm C thuộc d sao cho diện tích của tam giác ABC nhỏ nhất.

$A . C (- 1; 0; 2)$

$B . C (1; 1; 1)$

$C . C (- 3; - 1; 3)$

$D . C (- 5; - 2; 4)$

Câu 40:

Khẳng định nào sau đây là đúng?

A. $\int \tan x d x = - \ln | \cos x | + C$

$B . \int c o t x d x 〗 = - \ln | \sin x | + C$

$C . \int \sin \frac{x}{2} d x 〗 = 2 c o s \frac{x}{2} + C$

$D . \int c o s \frac{x}{2} d x 〗 = - 2 \sin \frac{x}{2} + C$

Câu 41:

Cho các số thực x, y thỏa mãn $x^{2} + 2 x y + 3 y^{2} = 4 .$ Giá trị lớn nhất của biểu thức $P = l o g_{2} (x - y)^{2}$ là:

$A . m a x P = 3 l o g_{2} 2$

$B . m a x P = l o g_{2} 12$

$C . m a x P = 12$

$D . m a x P = 16$

Câu 42:

Bạn A có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là 6cm, chiểu cao trong lòng cốc là 10cm đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Tính thể tích lượng nước trong cốc.

$A . 60 c m^{3}$

$B . 15 π c m^{3}$

$C . 70 c m^{3}$

$D . 60 π c m^{3}$

Câu 43:

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường $y = \sqrt{2 - x}, y = x, y = 0$ xung quanh trục Ox được tính theo công thức nào sau đây?

A. $V = π \int_{0}^{1} (2 - x) d x + π \int_{1}^{2} x^{2} d x$

B. $V = π \int_{0}^{2} (2 - x) d x$

C. $V = π \int_{0}^{1} x d x + π \int_{1}^{2} \sqrt{2 - x} d x$

D. $V = π \int_{0}^{1} x^{2} d x + π \int_{1}^{2} (2 - x) d x$

Câu 44:

Cho đồ thị hàm số y = f(x) có đồ thị đạo hàm như hình vẽ. Số điểm cực trị của đồ thị hàm số $y = f (x^{3})$ là:

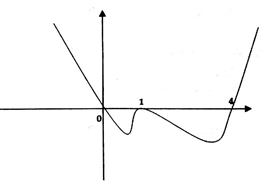
A. 0

B. 1

C. 2

D. 3

Câu 45:

Phương trình $s i n^{2} 3 x . c o s 2 x + s i n^{2} x = 0$ có bao nhiêu nghiệm thuộc (0;2017).

A. 2016

B. 1003

C. 1284

D. 1283

Câu 46:

Cho hàm số $f (n) = a \sqrt{n + 1} + b \sqrt{n + 2} + c \sqrt{n + 3}$ $(n \in ℕ *)$ với a, b, c là hằng số thỏa mãn a + b + c = 0. Khẳng định nào sau đây đúng?

A. $\underset{x \to + \infty}{l i m} f (n) = - 1$

B. $\underset{x \to + \infty}{l i m} f (n) = 1$

C. $\underset{x \to + \infty}{l i m} f (n) = 0$

D. $\underset{x \to + \infty}{l i m} f (n) = 2$

Câu 47:

Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết $\tan \frac{A}{2} \tan \frac{C}{2} = \frac{x}{y} (x, y \in N)$ , giá trị x + y là:

A. 4

B. 1

C. 2

D. 3

Câu 48:

Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức $u = \frac{z}{w}$ là:

A. $a = \frac{1}{4}$

B. a = 1

C. $a = \frac{1}{8}$

D. $a = - \frac{1}{8}$

Câu 49:

Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau và chia hết cho 15.

A. 222

B. 240

C. 200

D. 120

Câu 50:

Tổng các nghiệm của phương trình $1 + \log_{2} \sqrt{{(x + 1)}^{3}}$ $= \log_{2} (- x^{3} + 3 x^{2} + 3 x)$ có dạng $\frac{a + \sqrt{c}}{b} - b \sqrt{b} (a, b, c \in ℕ)$ . Giá trị a + b + c là:

A. 9

B. 10

C. 11

D. 12

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 3)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp đề thi thử THPTQG môn Tóan cực hay chọn lọc, có lời giải chi tiết (đề số 3)

CHỌN BỘ SÁCH BẠN MUỐN XEM