Tổng hợp đề thi thử THPTQG môn Toán mới nhất cực hay (Đề 15)

Câu 1:

Tính $\underset{x \to + \infty}{l i m} \frac{2 |x| + 3}{x - 1}$ .

A. -2.

B. 1.

B. -3.

D. 2.

Câu 2:

Phần ảo của số phức z=4+5i là

A. 5i.

B. 4.

C. 5.

C. 4i.

Câu 3:

Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây ?

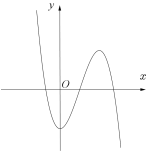
A. $y = x^{3} - 3 x^{2} - 2$ .

B. $y = - x^{3} + 3 x^{2} - 2$ .

C. $y = x^{3} + 3 x^{2} - 2$ .

D. $y = - x^{3} - 3 x^{2} - 2$ .

Câu 4:

Cho ab=100. Giá trị biểu thức log⁡a+log⁡b bằng

A. 2.

B. -2.

C. 10.

D. -10.

Câu 5:

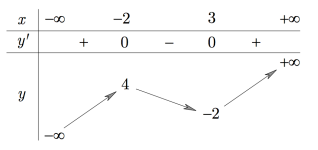
Cho hàm số f(x) có bảng biến thiên như hình vẽ bên

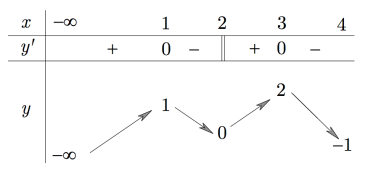
Số điểm cực trị của hàm số f(x) là

A. 2.

B. 4.

C. 3.

D. 5.

Câu 6:

Cho hình nón có bán kính đáy r, chiều cao h và đường sinh l. Mệnh đề nào dưới đây đúng ?

A. $l^{2} = r^{2} + h^{2}$ .

B. $h^{2} = r^{2} + l^{2}$ .

C. $r^{2} = h^{2} + l^{2}$ .

D. $l^{2} = r h$ .

Câu 7:

Họ các nguyên hàm của hàm số f(x)=cos⁡3x là

A. -3sin⁡3x+C.

B. $\frac{\sin 3 x}{3}$ +C.

C. 3sin⁡3x+C.

D. $- \frac{\sin 3 x}{3}$ +C.

Câu 8:

Cho hàm số f(x) có bảng biến thiên như hình vẽ bên

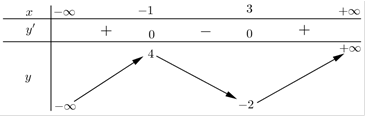
Hàm số f(x) đồng biến trên khoảng nào dưới đây ?

A. $(- \infty; 4)$ .

B. (-2;4).

C. $(- 2; + \infty)$ .

D. $(3; + \infty)$ .

Câu 9:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-2;0),B(-2;4;-2). Toạ độ trung điểm của đoạn thẳng AB là

A. (0;2;-2).

B. (0;4;-4).

C. (0;1;-1).

D. (-4;6;-2).

Câu 10:

Thể tích khối tròn xoay khi quay xung quanh trục Ox hình phẳng giới hạn bởi đường cong $y = \sqrt{4 - x^{2}}$ , trục hoành và hai đường thẳng x=0;x=2 là

A. $\frac{32}{3}$ $π$

B. $π^{2}$

C. 2 $π^{2}$

D. $\frac{16}{3}$ $π$

Câu 11:

Tập nghiệm của bất phương trình $2^{\frac{1}{x}} > \sqrt{2}$ là

A. $(2; + \infty)$ .

B. $(- \infty; 2)$ .

C. (0;2).

D. $(- \infty; 0) \cup (0; 2) .$

Câu 12:

Giá trị nhỏ nhất của hàm số $f (x) = l n (x^{2} + x + 1)$ trên đoạn [-2;0] bằng

A. ln⁡3.

B. 0.

C. -2 ln⁡2.

D. ln⁡3-2 ln⁡2.

Câu 13:

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d: $\frac{x - 3}{1} = \frac{y - 2}{2} = \frac{z - 1}{3}$ . Một véctơ chỉ phương của đường thẳng d là

A. $\vec{u_{1}}$ (1;2;3).

B. $\vec{u_{1}}$ (3;2;1).

C. $\vec{u_{1}}$ (1;3;2).

D. $\vec{u_{1}}$ (2;1;3).

Câu 14:

Cho hình lăng trụ đứng ABC.A′B′C′ có BB'=a và đáy là tam giác vuông cân tại B và AC= $a \sqrt{2}$ . Thể tích của khối lăng trụ đã cho bằng

A. $\frac{1}{3}$ $a^{3}$

B. $a^{3}$

C. $\frac{1}{2}$ $a^{3}$

D. $\frac{1}{6}$ $a^{3}$

Câu 15:

Đồ thị hàm số nào dưới đây có tiệm cận đứng ?

A. y = $\frac{1}{x^{2} + 1}$

B. y = $\frac{1}{x + \sqrt{x^{2} + 1}}$

C. y = $\frac{\sqrt{x^{2} + 1}}{x}$

D. y = $\frac{x^{2} - 1}{\sqrt{x - 1}}$

Câu 16:

Tích phân $\int_{\ln 2}^{\ln 3} e^{x + 1} d x$ bằng

A. 5e

B. e

C. e(ln3-ln2)

D. e(ln3+ln2)

Câu 17:

Có bao nhiêu số tự nhiên gồm bốn chữ số và các chữ số đôi một khác nhau

A. $9 . 10^{3}$

B. $A_{9}^{4}$

C. $A_{10}^{4}$

D. $9 . A_{9}^{3}$

Câu 18:

Số giao điểm của đồ thị hàm số $y = x^{4} - 3 x^{2} + 1$ với trục Ox là

A. 4.

B. 2.

C. 0.

D. 1.

Câu 19:

Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng qua điểm A(1;1;1) và vuông góc với đường thẳng d: $\{\begin{cases} x = 3 + t \\ y = 1 + 2 t \\ z = - 1 + 3 t \end{cases}$ là

A. 3x+y-z-3=0.

B. x+2y+3z-6=0.

C. 3x+y-z+3=0.

D. x+2y+3z+6=0.

Câu 20:

Gọi $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2} + 2 z + 2^{2018} = 0$ . Tính $| z_{1} | + | z_{2} |$ .

A. $2^{1009}$

B. $2^{1008}$

C. $2^{1010}$

D. $2^{1007}$

Câu 21:

Tổng số tiền ông A dùng để trả tiền thuê mặt bằng công ty trong năm 2017 là 200 triệu đồng. Biết cứ sau mỗi năm tổng số tiền dùng để trả tiền thuê mặt bằng công ty cho cả năm đó tăng thêm 10% so với năm trước. Tổng số tiền ông A dùng để trả tiền thuê mặt bằng công ty trong cả ba năm 2017, 2018 và 2019 là

A. 660 triệu đồng.

B. 728,2 triệu đồng.

C. 682 triệu đồng.

D. 662 triệu đồng.

Câu 22:

Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O,d(O,(SAB))=a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng SB và CD bằng

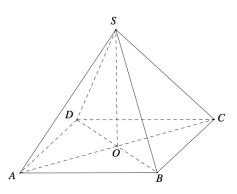
A. 2a

B. $\frac{3}{2}$ a

C. $\sqrt{3}$ a

D. $\sqrt{2}$ a

Câu 23:

Gieo một con xúc sắc cân đối, đồng chất hai lần. Xác suất để cả hai lần đều xuất hiện mặt sáu chấm bằng

A. $\frac{1}{36}$

B. $\frac{5}{36}$

C. $\frac{35}{36}$

D. $\frac{31}{36}$

Câu 24:

Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-2), B(3;-4;0), C(1;2;-1). Phương trình đường thẳng qua C và song song với AB là

A. $\{\begin{cases} x = 1 + t \\ y = 2 - 3 t \\ z = - 1 + t \end{cases}$

B. $\{\begin{cases} x = 1 + 2 t \\ y = 2 - t \\ z = - 1 - t \end{cases}$

C. $\{\begin{cases} x = 1 + t \\ y = 2 - t \\ z = - 1 + t \end{cases}$

D. $\{\begin{cases} x = 1 + 2 t \\ y = 2 - 3 t \\ z = - 1 - t \end{cases}$

Câu 25:

Tổng các nghiệm của phương trình $(l o g (10 x))^{2} - 3 l o g (100 x)$ $= - 5$ bằng

A. 11.

B. $\frac{11}{10}$ .

C. 110.

D. $\frac{101}{10}$ .

Câu 26:

Cho tứ diện OABC có OA,OB,OC đôi một vuông góc. Góc giữa mặt phẳng (ABC) và các đường thẳng OA,OB lần lượt là $30 °$ và $45 °$ . Tính góc giữa đường thẳng OC và mặt phẳng (ABC).

A. 45 $°$

B. 30 $°$

C. 60 $°$

D. 90 $°$

Câu 27:

Cho hình chóp S.ABC có tam giác SAB vuông cân tại S; tam giác ABC vuông cân tại C và $\hat{B S C} = 60^{0}$ . Gọi M là trung điểm cạnh SB. Côsin góc giữa hai đường thẳng AB và CM bằng

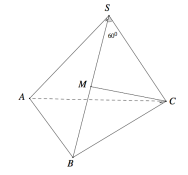
A. $\frac{\sqrt{6}}{6}$

B. $\frac{\sqrt{30}}{6}$

C. $\frac{\sqrt{6}}{3}$

D. $\frac{\sqrt{3}}{3}$

Câu 28:

Hệ số của số hạng chứa $x^{5}$ trong khai triển $(1 + x)^{5} (1 + x^{2})^{5}$ là

A. 65.

B. 101.

C. 135.

D. 155.

Câu 29:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;-2;0),B(-3;0;2) và mặt phẳng (P):x+y+z-5=0. Điểm M(a;b;c) trên (P) sao cho MA=MB= $3 \sqrt{2}$ . Tính ab+bc+ca.

A. 5

B. 1

C. 7

D. 3

Câu 30:

Có bao nhiêu số nguyên m<10 để hàm số $y = x^{3} - 3 x^{2} + m x - 1$ đồng biến trên khoảng $(0; + \infty)$ .

A. 13.

B. 6.

C. 7.

D. 3.

Câu 31:

Cho số phức $z = m - 2 + (m^{2} - 1) i$ , với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z nằm trên đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.

A. $\frac{1}{3}$

B. $\frac{8}{3}$

C. $\frac{4}{3}$

D. $\frac{2}{3}$

Câu 32:

Cho $\int_{1}^{2} (x + 1) / (x^{2} + x l n x) d x$ =ln⁡(ln⁡a+b) với a,b là các số nguyên dương. Giá trị biểu thức ab+a+b bằng

A. 8.

B. 11.

C. 15.

D. 7.

Câu 33:

Trên đoạn [1;4] các hàm số $f (x) = x^{2} + p x + q$ ; $g (x) = x + \frac{4}{x^{2}}$ có cùng giá trị nhỏ nhất và đạt tại cùng một điểm. Hỏi giá trị lớn nhất của hàm số f(x) trên đoạn [1;4] là?

A. 4.

B. 7.

C. 11.

D. 9.

Câu 34:

Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD=8,CD=6,AC'=12. Tính diện tích toàn phần $S_{t p}$ của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′.

A. $S_{t p}$ = 576 $π$

B. $S_{t p}$ = $10 (2 \sqrt{11} + 5)$ $π$

C. $S_{t p}$ = 26 $π$

D. $S_{t p}$ = $5 (4 \sqrt{11} + 5)$ $π$

Câu 35:

Có bao nhiêu số nguyên m để phương trình $(c o s 3 x + m)^{3} + 2 m = 10 c o s x$ có nghiệm thực.

A. 3.

B. 2.

C. 5.

D. 9.

Câu 36:

Có bao nhiêu số nguyên $m \in (0; 2018)$ để phương trình $m + 10 x = m e^{x}$ có hai nghiệm phân biệt.

A. 2017.

B. 2016.

C. 9.

D. 2007.

Câu 37:

Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây

Có bao nhiêu số nguyên m để hàm số y=f(x+m) nghịch biến trên khoảng (0;1).

A. 3.

B. 5.

C. 1.

D. 4.

Câu 38:

Cho số phức z thoả mãn |z|=2 và $| z^{2} + 1 | = 4$ . Tính $| z + z | + | z - z |$ .

A. 16.

B. $7 + \sqrt{3}$ .

C. $3 + 2 \sqrt{2}$ .

D. $3 + \sqrt{7}$ .

Câu 39:

Trong không gian với hệ toạ độ Oxyz, biết rằng có n mặt phẳng dạng $(P_{i})$ : $x + a_{i} y + b_{i} z + c_{i}$ =0 (i=1,2,...,n) đi qua điểm M(1;2;3) và cắt các trục toạ độ lần lượt tại A,B,C khác gốc toạ độ O sao cho O.ABC là hình chóp đều. Giá trị của biểu thức $S = a_{1} + a_{2} + . . . + a_{n}$ bằng

A. 1.

B. 3.

C. -3.

D. -1.

Câu 40:

Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A),(B),(C),(D) giới hạn bởi đồ thị hàm số f (x) và trục hoành lượt bằng 6;3;12;2. Tích phân $\int_{- 3}^{1} (2 f (2 x + 1) + 1) d x$ bằng

A. 27.

B. 25.

C. 17.

D. 21.

Câu 41:

Tìm giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 2 (m + 1) x^{2} + 2 m + 3$ ba điểm cực trị A,B,C sao cho trục hoành chia tam giác ABC thành hai đa giác sao cho: tỉ số giữa diện tích của tam giác nhỏ được chia ra và diện tích tam giác ABC bằng $\frac{4}{9}$ .

A. m = $\frac{- 1 + \sqrt{15}}{2}$

B. m = $\frac{- 1 + \sqrt{3}}{2}$

C. m = $\frac{5 + \sqrt{3}}{2}$

D. m = $\frac{1 + \sqrt{15}}{2}$

Câu 42:

Cho cấp số cộng $(u_{n})$ có tất cả các số hạng đều dương thoả mãn $u_{1} + u_{2} + . . . + u_{2018}$ $= 4 (u_{1} + u_{2} + . . . + u_{1009})$ . Giá trị nhỏ nhất của biểu thức P= $\log_{3}^{2} u_{2} + \log_{3}^{2} u_{5} + \log_{3}^{2} u_{14}$ bằng

A. 2.

B. 1.

C. 3.

D. 4.

Câu 43:

Cho hàm số $y = \frac{2 x}{x + 1}$ có đồ thị (C) và điểm A(0;a). Gọi S là tập hợp tất cả các giá trị thực của a để từ A kẻ được hai tiếp tuyến AM, AN đến (C) với M,N là các tiếp điểm và MN=4. Tổng các phần tử của S bằng

A. 4.

B. 3.

C. 6.

D. 8.

Câu 44:

Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-1),B(2;0;1),C(-2;2;3). Đường thẳng $Δ$ nằm trong mặt phẳng (ABC) qua trực tâm H của tam giác ABC và cùng tạo với các đường thẳng AB, AC một góc $α < 45 °$ có một véctơ chỉ phương là $\vec{u}$ (a;b;c) với c là một số nguyên tố. Giá trị của biểu thức ab+bc+ca bằng

A. -67.

B. 23.

B. -33.

B. -37.

Câu 45:

Cho số phức z. Giá trị nhỏ nhất của biểu thức P=3|z+i|+3|z-i|+|z+ $z$ -2| bằng

A. 4+ $2 \sqrt{3}$

B. 2+ $\sqrt{3}$

C. 2+ $\sqrt{5}$

D. 2+ $4 \sqrt{2}$

Câu 46:

Cho hàm số f(x) có đạo hàm liên tục trên đoạn [1;4] thỏa mãn f(1)=-1, f(4)=-8 và $\sqrt{x^{3}} (f^{'} (x))^{2} - f (x)$ $= 9 \sqrt{x^{3}} - \sqrt{x} - 3 x$ , $\forall x \in [1; 4]$ . Tích phân $\int_{1}^{4} f (x) d x$ bằng

A. -7

B. $- \frac{89}{6}$

C. $- \frac{79}{6}$

D. -8

Câu 47:

Có 4 bóng xanh, 5 bóng đỏ và 6 bóng vàng. Chọn ngẫu nhiên ra 6 bóng, xác suất để chọn được 6 bóng có đủ 3 màu bằng

A. $\frac{757}{5005}$

B. $\frac{151}{1001}$

C. $\frac{850}{1001}$

D. $\frac{4248}{5005}$

Câu 48:

Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB=3,BC=4. Tam giác SAC nằm trong mặt phẳng vuông góc với đáy, d(C,SA)=4.. Côsin góc giữa hai mặt phẳng (SAB) và (SAC) bằng

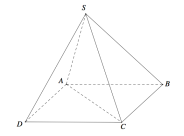
A. $\frac{5 \sqrt{34}}{34}$

B. $\frac{3 \sqrt{17}}{17}$

C. $\frac{2 \sqrt{34}}{17}$

D. $\frac{3 \sqrt{34}}{34}$

Câu 49:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-3=0. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.

A. $\sqrt{21}$ .

B. $2 \sqrt{6}$ .

C. 6.

D. $3 \sqrt{3}$ .

Câu 50:

Cho hình chóp S.ABC có AB=a,AC= $\sqrt{3} a$ ,SB>2a và $\hat{A B C} = \hat{B A S} = \hat{B C S}$ $= 90^{0}$ . Sin của góc giữa đường thẳng SB và mặt phẳng (SAC) bằng $\frac{\sqrt{11}}{11}$ . Tính thể tích khối chóp S.ABC.

A. $\frac{\sqrt{6}}{6}$ $a^{3}$

B. $\frac{\sqrt{6}}{3}$ $a^{3}$

C. $\frac{\sqrt{3}}{9}$ $a^{3}$

D. $\frac{2 \sqrt{3}}{9}$ $a^{3}$

Tổng hợp đề thi thử THPTQG môn Toán mới nhất cực hay (Đề 15)

Giới thiệu

Liên kết

Chính sách

Kết nối

Tổng hợp đề thi thử THPTQG môn Toán mới nhất cực hay (Đề 15)

CHỌN BỘ SÁCH BẠN MUỐN XEM