Tổng hợp đề thi thử THPTQG môn Toán mới nhất cực hay (Đề 3)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z.

A. Phần thực bằng 3 và phần ảo bằng 2.
B. Phần thực bằng 3 và phần ảo bằng -2.
C. Phần thực bằng 3 và phần ảo bằng 2i.
D. Phần thực bằng 3 và phần ảo bằng -2i.
Tính .
A.
B. 0.
C.
D.
Số chỉnh hợp chập 3 của 10 phần tử bằng
A.
B.
C.
D. 10! - 3!
Thể tích của khối lập phương có độ dài cạnh bằng 6 là
A. 72.
B. 216.
C. 108.
D. 36.
Hàm số nào dưới đây đồng biến trên khoảng ?
A.
B. .
C.
D.
Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường quanh trục hoành bằng
A. V =
B. V =
C. V =
D. V =
Cho hàm số y=f(x) xác định và liên tục trên R. Biết đồ thị của hàm số f'(x) như hình vẽ. Các điểm cực đại của hàm số y=f(x)trên đoạn [0;3] là

A. x=0 và x=2.
B. x=1 và x=3.
C. x=2.
D. x=0.
Cho a,b là hai số thực dương bất kì. Mệnh đề nào dưới đây đúng ?
A. ln(ab)=lna.lnb
B.
C.
D.
Họ nguyên hàm của hàm số là:
A. + C
B. + C
C. + C
D. + C
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;0;-2), B(4;0;0). Tâm đường tròn ngoại tiếp tam giác OAB là
A. M(0;4;-2).
B. N(4;0;-2).
C. P(2;0;-1).
D. Q(0;2;-1)
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây ?
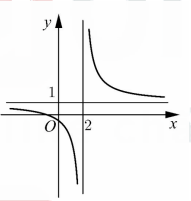
A. y =
B. y =
C. y =
D. y =
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:. Đường thẳng d đi qua điểm nào dưới đây ?
A. M(-1;2;1).
B. N(2;1;1).
C. P(-2;-1;0).
D. Q(2;1;0).
Tập nghiệm của bất phương trình là
A. (0;3).
B. .
C. .
D. .
Cho hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tìm chiều cao của hình nón.
A. h =
B. h =
C. h =
D. h =
Trong không gian với hệ tọa độ Oxyz, mặt phẳng qua điểm A(1;2;3) và song song với mặt phẳng toạ độ (Oxy) có phương trình là
A. x-1=0.
B. y-2=0.
C. z+3=0.
D. z-3=0.
Tiệm cận ngang của đồ thị hàm số là
A. y = 0
B. y = 1
C. y = 2
D. y = 3
Đường cong ở hình vẽ bên là đồ thị của hàm số y=f(x).

Số nghiệm của phương trình 2f(x)-1=0 là
A. 2.
B. 4.
C. 0.
D. 3.
Giá trị nhỏ nhất của hàm số trên đoạn [-2;2] bằng
A. -2
B. 0.
C. -1
D. 2.
Tích phân bằng
A.
B.
C.
D.
Cho phương trình có một nghiệm phức z=3-2i. Nghiệm phức còn lại của phương trình là
A. 3+2i
B. -3-2i.
C. -3+2i.
D. 2+3i.
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình thoi và các góc đỉnh A bằng (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
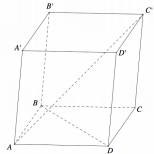
A. 90
B. 30
C. 45
D. 60
Theo một bài báo được công bố trên tạp chí Nature, trung bình làm cha ở 30 tuổi sẽ có 55 đột biến cho con cái của mình. Đột biến này tăng theo độ tuổi. Cứ tăng 1 tuổi, số lượng đột biến sẽ tăng thêm 12% so với số lượng đột biến ở độ tuổi trước đó. Hỏi sau đúng 50 năm, tức ở độ tuổi 80 lượng đột biến là bao nhiêu ?
A. 17802.
B. 15895.
C. 14450.
D. 16184.
Có 8 người cùng vào thang máy của một toà nhà gồm 13 tầng, mỗi người sẽ đi ra ngẫu nhiên ở một trong 13 tầng. Xác suất để mỗi người ra ở một tầng khác nhau bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;-1;1). Gọi lần lượt là hình chiếu vuông góc của M lên các trục y'Oy, z'Oz. Đường thẳng có véctơ chỉ phương nào dưới đây ?
A. (0;1;1).
B. (3;1;0).
C. (0;-1;1).
D. (3;-1;0).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
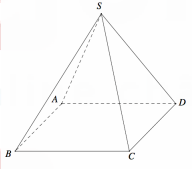
A.
B.
C.
D.
Có tất cả bao nhiêu số hạng mà luỹ thừa của x nguyên trong khai triển ?
A. 3.
B. 1.
C. 4.
D. 2.
Tổng các nghiệm của phương trình là:
A. 10010.
B. .
C. 110.
D. .
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh AC (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BM và mặt phẳng (BCD) bằng
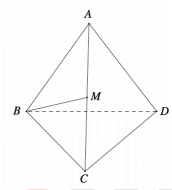
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;2;1), B(-2;1;3), C(2;-1;3), D(0;3;1). Mặt phẳng (P):ax+by+cz-10=0 đi qua hai điểm A, B và cách đều hai điểm C, D và hai điểm C, D nằm khác phía so với mặt phẳng (P). Tính S=a+b+c.
A. S=7.
B. S=15.
C. S=6.
D. S=13.
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số đồng biến trên khoản ?
A. 3.
B. 0.
C. 2.
D. 4.
Cho (H) là hình phẳng giới hạn bởi parabol , cung tròn có phương trình (với ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
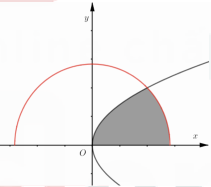
A.
B.
C.
D.
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn Giá trị của biểu thức bằng
A. -2
B. -1
C. 2.
D. 1.
Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).
A. 60
B. 30
C. 45
D. 15
Phương trình có tất cả bao nhiêu nghiệm thực ?
A. 1.
B. 0.
C. 2018.
D. 2019.
Có bao nhiêu số nguyên m để phương trình m+sin(m+sin3x) = sinx(3sinx )+4 có nghiệm thực.
A. 9.
B. 5.
C. 4.
D. 8.
Cho hàm số , với m là tham số thực. Hàm số đã cho có thể có nhiều nhất bao nhiêu điểm cực trị ?
A. 3.
B. 1.
C. 2.
D. 4.
Số phức z=a+bi có |z|= và có phần ảo bằng 8, điểm biểu diễn số phức z nằm trong góc phần tư thứ ba của hệ trục toạ độ. Giá trị của biểu thức P=a+b bằng
A. P=4.
B. P=0.
C. P=-4.
D. P=2.
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng x=2 kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số .
A. 7.
B. 3.
C. 9.
D. 8.
Cho hàm số y=f(x) có đạo hàm , trong đó . Hàm số đồng biến trên khoảng nào dưới đây?
A. .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(3;1;3), mặt phẳng (P):x+y+z-7=0 và đường thẳng (d): Mặt cầu (S) có tâm I(a;b;c) thuộc (P), bán kính R= và tiếp xúc với (d) tại A với a,b,c là các số thực dương. Giá trị của biểu thức a+2b+3c bằng
A. 11.
B. 17.
C. 16.
D. 12.
Gọi S là tập hợp các số phức z thoả mãn và . Kí hiệu là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính .
A. 5
B.
C.
D. 10
Cho hàm số y=f(x) xác định và liên tục trên R thỏa mãn với mọi . Tích phân bằng
A. 10.
B. .
C. 72.
D. 2.
Cho hàm số . Có bao nhiêu số nguyên dương m < 2018 sao cho với mọi bộ ba số thực a,b,c[-1;3] thì f(a),f(b),f(c) là độ dài ba cạnh một tam giác nhọn.
A. 2009.
B. 2013.
C. 2017.
D. 2008.
Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng có phương trình , ; , . Biết rằng đường thẳng có véctơ chỉ phương (2;b;c)cắt cả bốn đường thẳng đã cho. Giá trị của biểu thức 2a+3b bằng
A. 5.
B. -1.
C. .
D. .
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó EF=2a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF.
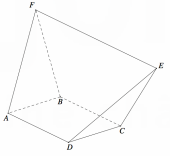
A. V =
B. V =
C. V =
D. V =
Cho dãy số () xác định bởi , với mọi . Tìm số nguyên nhỏ nhất thỏa mãn
A. 146.
B. 233.
C. 232.
D. 147.
Cho hình lăng trụ tam giác đều ABC.A′B′C’ có AB=2, AA'=2 (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng AB’ và A’C
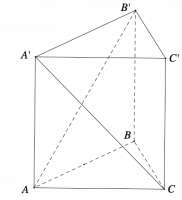
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x-2y+2z-3=0 và hai điểm A(1;2;3),B(3;4;5).Gọi M là một điểm di động trên (P). Giá trị lớn nhất của biểu thức bằng
A.
B.
C.
D.
Chọn ngẫu nhiên ba số từ tập A={1,2,3,...,100}. Xác suất để chọn được ba số mà các số đó lập thành một cấp số nhân tăng có công bội là một số nguyên dương bằng
A.
B.
C.
D.
Cho hàm số y=f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt . Biết với mọi . Tích phân có giá trị lớn nhất bằng
A.
B. 4.
C.
D. 5.