Ứng dụng tích phân để tính thể tích
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hình (H) giới hạn bởi đồ thị hàm số y=f(x) , trục hoành và hai đường thẳng x=a,x=b. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox là:
A.\[V = \pi \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
B. \[V = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
C. \[V = \pi \mathop \smallint \limits_a^b {f^2}\left( x \right)dx\]
D. \[V = {\pi ^2}\mathop \smallint \limits_a^b {f^2}\left( x \right)dx\]
Cho hình (H) giới hạn bởi đồ thị hàm số \[y = {x^3}\], trục hoành và hai đường thẳng x=0,x=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:
A.\[V = {\pi ^2}\mathop \smallint \limits_0^1 {x^3}dx\]
B. \[V = \pi \mathop \smallint \limits_0^1 {x^3}dx\]
C. \[V = \pi \mathop \smallint \limits_0^1 {x^6}dx\]
D. \[V = \pi \mathop \smallint \limits_0^1 {x^5}dx\]
Cho hình (H) giới hạn bởi đường cong \[{y^2} + x = 0\], trục Oy và hai đường thẳng y=0,y=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính bởi:
A.\[V = {\pi ^2}\mathop \smallint \limits_0^1 {x^4}dx\]
B. \[V = \pi \mathop \smallint \limits_0^1 {y^2}dy\]
C. \[V = \pi \mathop \smallint \limits_0^1 {y^4}dy\]
D. \[V = \pi \mathop \smallint \limits_0^1 - {y^4}dy\]
Cho hình phẳng (H) giới hạn bởi \[y = \frac{1}{3}{x^3} - {x^2}\;\] và Ox. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox bằng :
A.\[\frac{{81\pi }}{{35}}\]
B. \[\frac{{53\pi }}{6}\]
C. \[\frac{{81}}{{35}}\]
D. \[\frac{{21\pi }}{5}\]
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y = 2(x - 1){e^x}\], trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox .
A.\[V = 4 - 2e\]
B. \[V = \left( {4 - 2e} \right)\pi \]
C. \[V = {e^2} - 5\]
D. \[V = \left( {{e^2} - 5} \right)\pi \]
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \[y = {x^2} + 1;x = 0\] và tiếp tuyến của đồ thị hàm số \[y = {x^2} + 1\;\] tại điểm A(1;2) quanh trục Ox là
A.\[\frac{2}{5}\pi \]
B. \(\pi \)
C. \[\frac{1}{2}\pi \]
D. \[\frac{8}{{15}}\pi \]
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \[y = \sqrt x ,y = 0\;\] và x=4 quanh trục Ox . Đường thẳng \[x = a(0 < a < 4)\;\] cắt đồ thị hàm số \[y = \sqrt x \;\] tại M (hình vẽ bên).
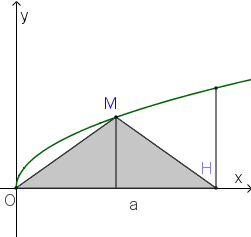
A.\[a = 2\sqrt 2 \]
B. \[a = \frac{5}{2}\]
C. \[a = 2\]
D. \[a = 3\]
Cho hai hàm số \[y = {f_1}\left( x \right)\]và\(y = {f_2}\left( x \right)\) liên tục trên đoạn \[\left[ {a;b} \right]\;\]và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ?
![Cho hai hàm số y = f 1 ( x ) và y = f 2 ( x ) liên tục trên đoạn [ a ; b ] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ? y = f 1 ( x ) và y = f 2 ( x ) liên tục trên đoạn [ a ; b ] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ? (ảnh 1)](https://video.vietjack.com/upload2/images/1656411446/1656411669-image2.png)
A.\[V = \pi \mathop \smallint \limits_a^b \left( {f_1^2(x) - f_2^2(x)} \right)dx\]
B. \[V = \pi \mathop \smallint \limits_a^b \left( {{f_1}(x) - {f_2}(x)} \right)dx\]
C. \[V = \mathop \smallint \limits_a^b \left( {f_1^2(x) - f_2^2(x)} \right)dx\]
D. \[V = \pi \mathop \smallint \limits_a^b {\left( {{f_1}(x) - {f_2}(x)} \right)^2}dx\]Trả lời:
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \[y = \sqrt {2 - x} ;y = x\] xung quanh trục Ox được tính theo công thức nào sau đây?
A.\[V = \pi \mathop \smallint \limits_0^2 (2 - x)dx + \pi \mathop \smallint \limits_0^2 {x^2}dx\]
B. \[V = \pi \mathop \smallint \limits_0^2 (2 - x)dx\]
C. \[V = \pi \mathop \smallint \limits_0^1 xdx + \pi \mathop \smallint \limits_1^2 \sqrt {2 - x} dx\]
D. \[V = \pi \mathop \smallint \limits_0^1 {x^2}dx + \pi \mathop \smallint \limits_1^2 (2 - x)dx\]
Cho vật thể V được giới hạn bởi hai mặt phẳng x=a và x=b(a<b), mặt phẳng vuông góc với trục Ox cắt V theo thiết diện S(x). Thể tích của V được tính bởi:
A.\[V = \mathop \smallint \limits_a^b S\left( x \right)dx\]
B. \[V = \pi \mathop \smallint \limits_a^b S\left( x \right)dx\]
C. \[V = \mathop \smallint \limits_a^b {S^2}\left( x \right)dx\]
D. \[V = \pi \mathop \smallint \limits_a^b {S^2}\left( x \right)dx\]
Cho vật thể V được giới hạn bởi hai mặt phẳng x=0 và x=−2, mặt phẳng vuông góc với trục Ox cắt V theo thiết diện \[S(x) = 2{x^2}\]. Thể tích của V được tính bởi:
A.\[V = \mathop \smallint \limits_{ - 2}^0 4{x^4}dx\]
B. \[V = \mathop \smallint \limits_0^{ - 2} 2{x^2}dx\]
C. \[V = \mathop \smallint \limits_{ - 2}^0 2{x^2}dx\]
D. \[V = \pi \mathop \smallint \limits_{ - 2}^0 4{x^4}dx\]
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \[x\;(1 \le x \le 3)\] thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và \[\sqrt {3{x^2} - 2.} \]
A.\[V = 32 + 2\sqrt {15} \]
B. \[V = \frac{{124\pi }}{3}\]
C. \[V = \frac{{124}}{3}\]
D. \[V = (32 + 2\sqrt {15} )\pi \]
Cho hình phẳng giới hạn bởi \[D = \left\{ {y = \tan x;\,\,y = 0;\,\,x = 0;\,\,x = \frac{\pi }{3}} \right\}.\] Thể tích vật tròn xoay khi D quay quanh trục Ox là \[V = \pi (a - \frac{\pi }{b}),\;\] với a,b∈R.. Tính \[T = {a^2} + 2b.\].
A.T=6.
B.T=9.
C.T=12.
D.T=3.
Tính thể tích khi \[S = \left\{ {y = {x^2} - 4x + 6;\,\,y = - \,{x^2} - 2x + 6} \right\}\] quay quanh trục Ox.
A.\[V = 3.\]
B. \[V = \frac{\pi }{3}.\]
C. \[V = \pi .\]
D. \[V = 3\pi .\]
Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh Ox của hình giới hạn bởi trục Ox và parabol \[(P):y = {x^2} - ax(a > 0)\;\]bằng V=2. Khẳng định nào dưới đây đúng ?
A.\[a \in \left( {\frac{1}{2};1} \right).\]
B.\[a \in \left( {1;\frac{3}{2}} \right).\]
C. \[a \in \left( {\frac{3}{2};2} \right).\]
D. \[a \in \left( {2;\frac{5}{2}} \right).\]
Cho hình phẳng (H) giới hạn bởi các đường \[y = - {x^2} + 2x\;\] và y=0. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Oy là
A.\[V = \frac{7}{3}\pi .\]
B. \[V = \frac{8}{3}\pi .\]
C. \[V = \frac{{10}}{3}\pi .\]
D. \[V = \frac{{16}}{3}\pi .\]
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường \[\left( E \right):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\]quay quanh Oy?
A.\[V = 36\pi .\]
B. \[V = 24\pi .\]
C. \[V = 16\pi .\]
D. \[V = 64\pi .\]
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị \[y = - \,\sqrt {4 - {x^2}} ,\,\,{x^2} + 3y = 0\] quay quanh trục Ox là \[V = \frac{{a\pi \sqrt 3 }}{b}\], với a,b> và \(\frac{a}{b}\) là phân số tối giản. Tính tổng T=a+b.
A.T=33.
B.T=31.
C.T=29.
D.T=27.
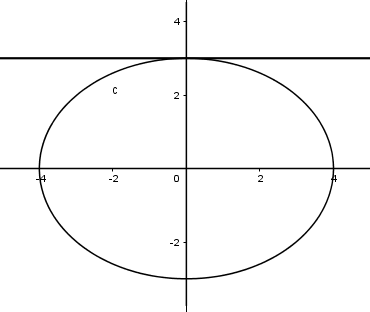
Tính thể tích hình xuyến do quay hình tròn có phương trình \[{x^2} + {\left( {y - 2} \right)^2} = 1\] khi quanh trục Ox..
A.\[V = 6{\pi ^2}.\]
B. \[V = 4{\pi ^2}.\]
C. \[V = 2{\pi ^2}.\]
D. \[V = 8{\pi ^2}.\]
Gọi (D1) là hình phẳng giới hạn bởi các đường \[y = 2\sqrt x ,y = 0\;{\rm{ }}v\`a \;x = 2020,\], (D2) là hình phẳng giới hạn bởi các đường \[y = \sqrt {3x} ,y = 0\] và \[x = 2020.\]. Gọi V1,V2 lần lượt là thể tích khối tròn xoay tạo thành khi quay (D1) và (D2) xung quanh trục Ox. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
A.\[\frac{4}{3}\]
B. \[\frac{{2\sqrt 3 }}{3}\]
C. \[\frac{2}{3}\]
D. \[\frac{{\sqrt 6 }}{3}\]