Câu hỏi:
323 lượt xem4. Thực hành trải nghiệm trong phòng máy
Thực hiện vẽ hình với phần mềm GeoGebra.
- Vẽ đường tròn (A; R) và điểm B nằm ngoài đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy rằng M thay đổi trên một nhánh hypebol.
Các bước thực hiện như sau:
Bước 1: Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2: Vẽ đường tròn (A; R):
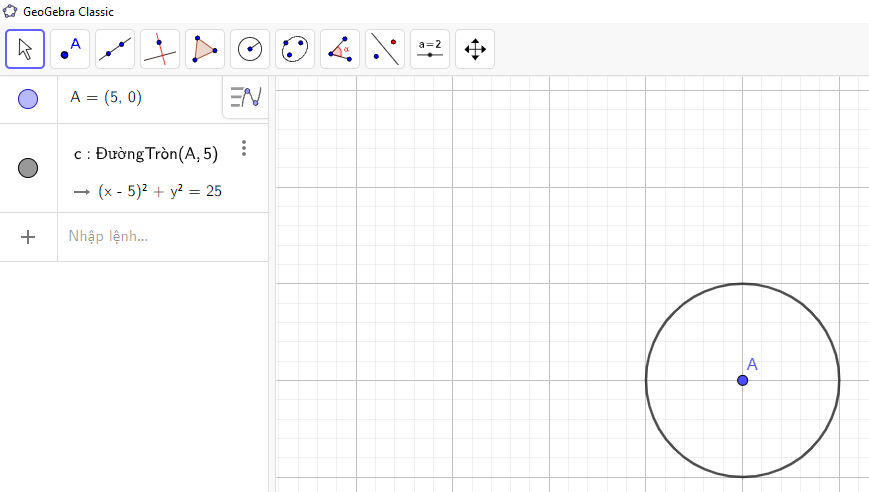
Chẳng hạn, lấy R = 5, ta vẽ đường tròn (A; 5) như sau: Trên thanh công cụ chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào một điểm bất kì trên vùng làm việc để có tâm A → Nhập số 5 ứng với bán kính của đường tròn như hình vẽ dưới đây:
→ Nhấn chuột trái vào một điểm bất kì trên vùng làm việc để có tâm A → Nhập số 5 ứng với bán kính của đường tròn như hình vẽ dưới đây:

Nhấn “OK”, ta được đường tròn như hình vẽ:
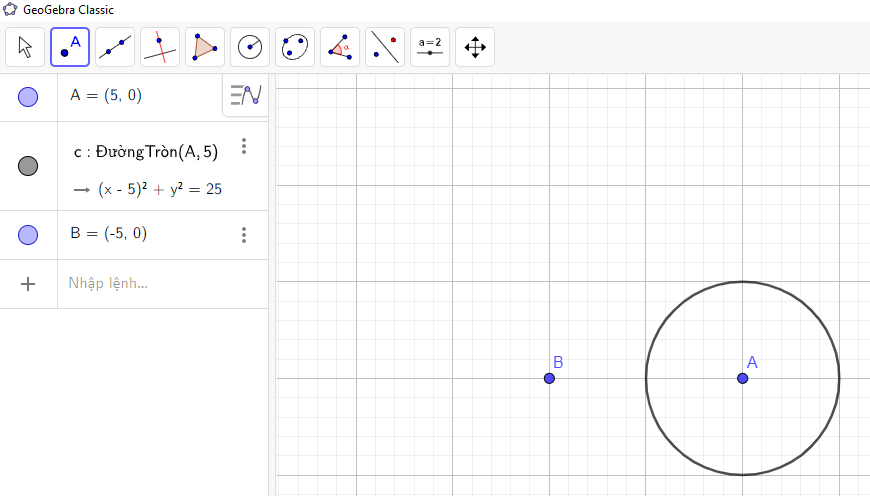
Bước 3: Lấy 1 điểm B bất kì nằm ngoài đường tròn.
Trên thanh công cụ ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào một điểm nằm ngoài đường tròn như hình vẽ:
→ Nhấn chuột trái vào một điểm nằm ngoài đường tròn như hình vẽ:
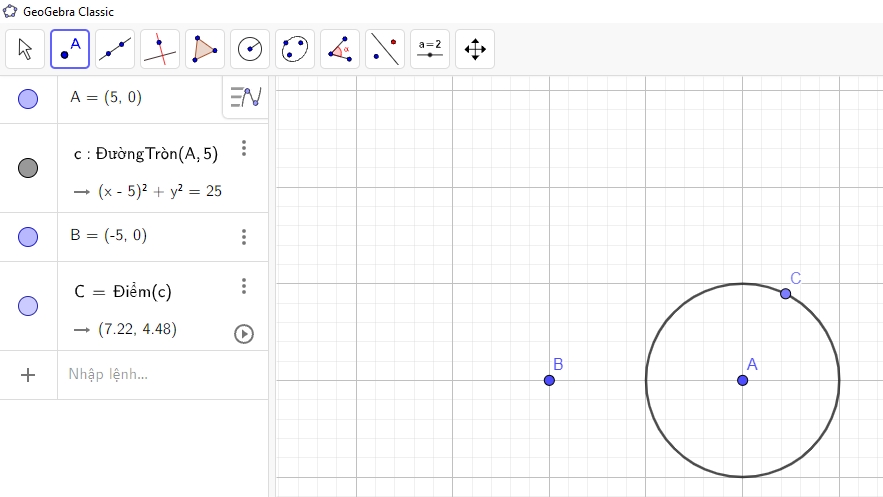
Bước 4: Lấy một điểm C trên đường tròn:
Ta nhấn chuột trái vào một điểm trên đường tròn đã vẽ, ta được điểm C như hình vẽ:
Bước 5: Vẽ đường thẳng AC
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào hai điểm A và C ta được hình vẽ:
→ Nhấn chuột trái vào hai điểm A và C ta được hình vẽ:
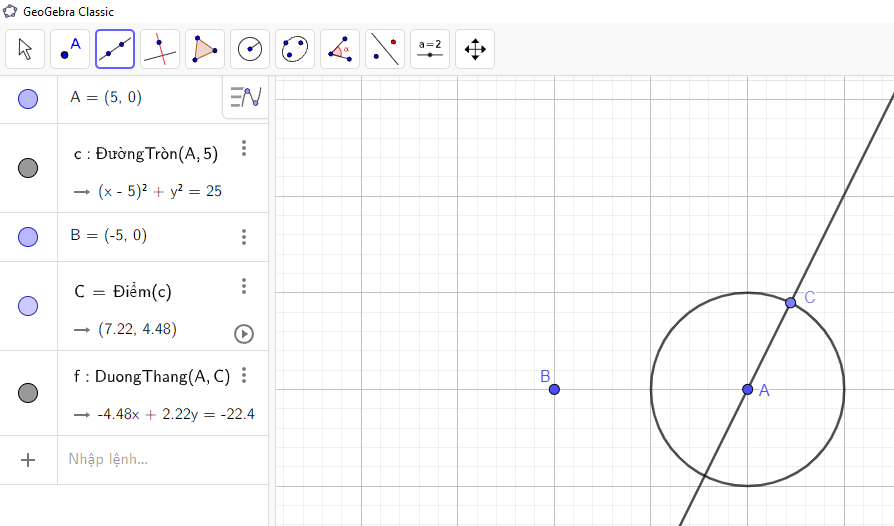
Bước 6: Vẽ đoạn thẳng BC:
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào điểm B và điểm C ta được hình vẽ:
→ Nhấn chuột trái vào điểm B và điểm C ta được hình vẽ:
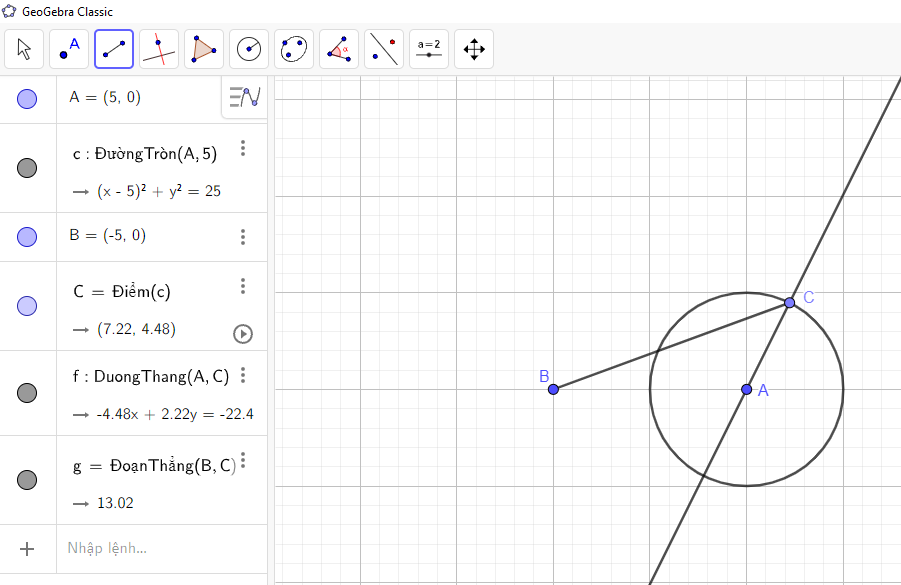
Bước 7: Vẽ đường trung trực của đoạn thẳng BC:
Trên thanh công cụ, chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào hai điểm B và C ta được như hình vẽ:
→ Nhấn chuột trái vào hai điểm B và C ta được như hình vẽ:
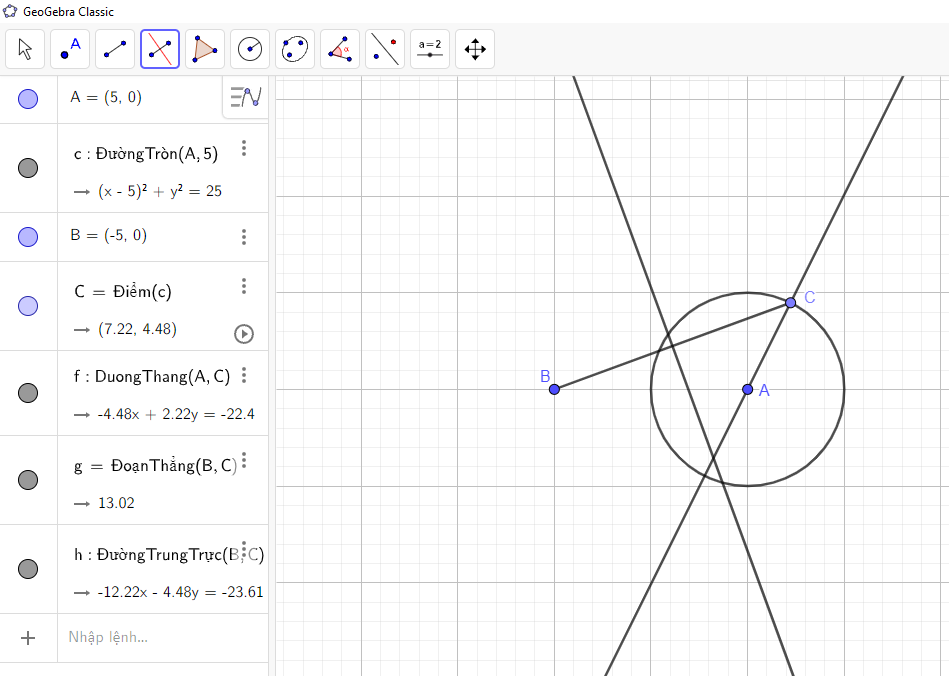
Bước 8: Lấy giao điểm của AC và trung trực của đoạn thẳng BC:
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào đường thẳng AC và trung trực đoạn thẳng BC ta được như hình vẽ:
→ Nhấn chuột trái vào đường thẳng AC và trung trực đoạn thẳng BC ta được như hình vẽ:
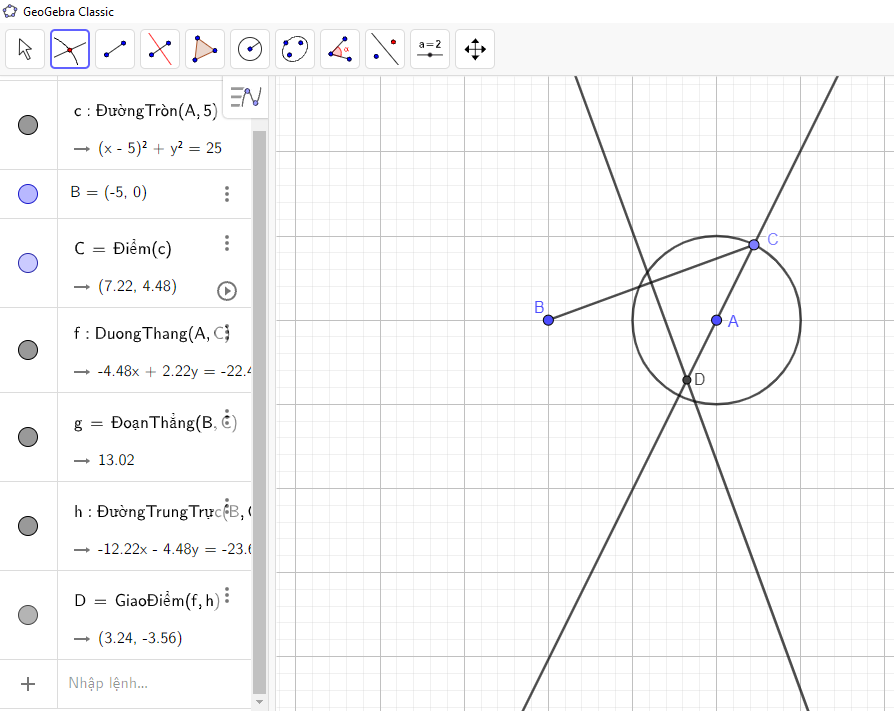
Bước 9: Đổi tên giao điểm D thành giao điểm M:
Trên thanh công cụ, chọn ![]() → Nhấn chuột trái vào điểm D → Nhấn chuột phải → Chọn
→ Nhấn chuột trái vào điểm D → Nhấn chuột phải → Chọn ![]() để đổi D thành M.
để đổi D thành M.

Nhấn “OK”, ta được như hình vẽ:
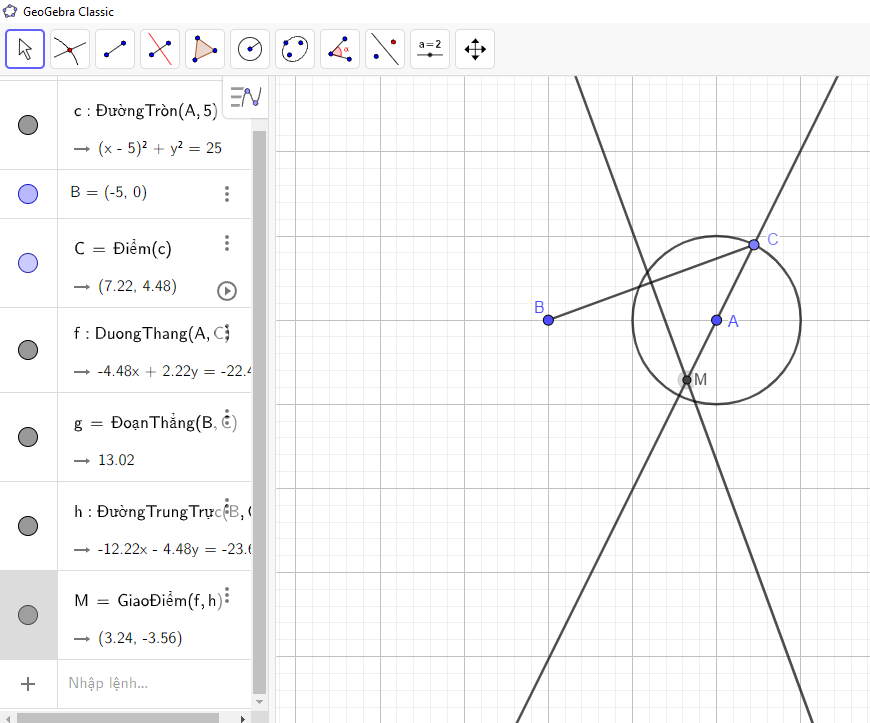
Bước 10: Cho điểm M hiện thị dấu vết khi di chuyển:
Nhấn chuột trái chọn điểm M → Nhấn chuột phải → Chọn ![]()
Bước 11: Cho điểm C di chuyển trên đường tròn (A; R):
Nhấn chuột trái chọn điểm C → Nhấn chuột phải → Chọn ![]()
Khi đó điểm C di chuyển dẫn đến M di chuyển trên một hypebol như hình vẽ
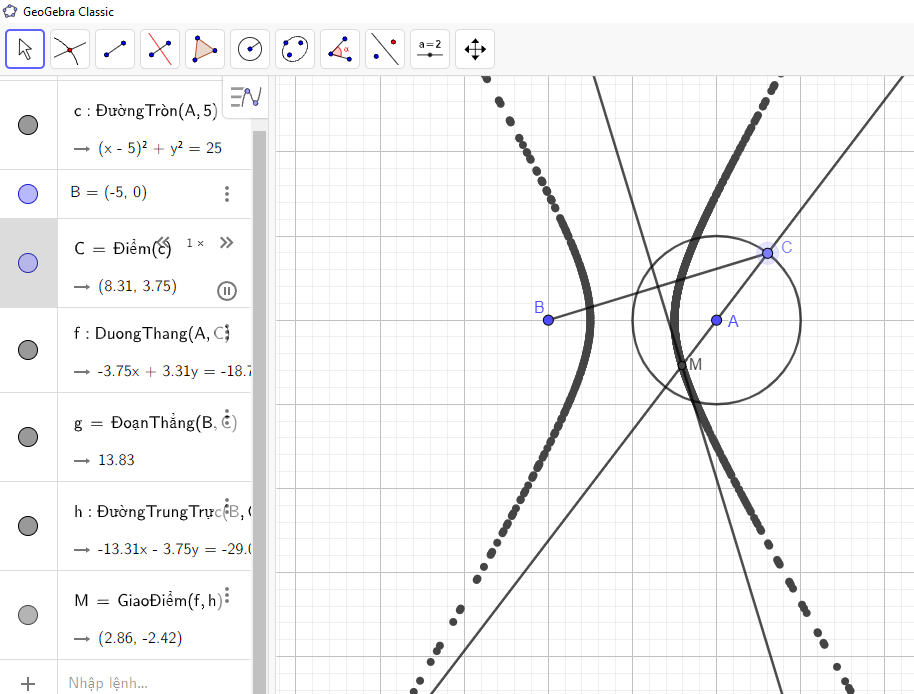
- Tương tự ta thực hiện các hình vẽ sau:
- Vẽ đường tròn (A; R) và điểm B nằm trong đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường tròn trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy M thay đổi trên một elip.
Vẽ tương tự như hoạt động trên, chỉ khác tại Bước 3, điểm B thay vì nằm ngoài đường tròn thì ta lấy bên trong đường tròn.
Khi đó, điểm C di chuyển thì ta được M chạy trên một elip như hình vẽ:
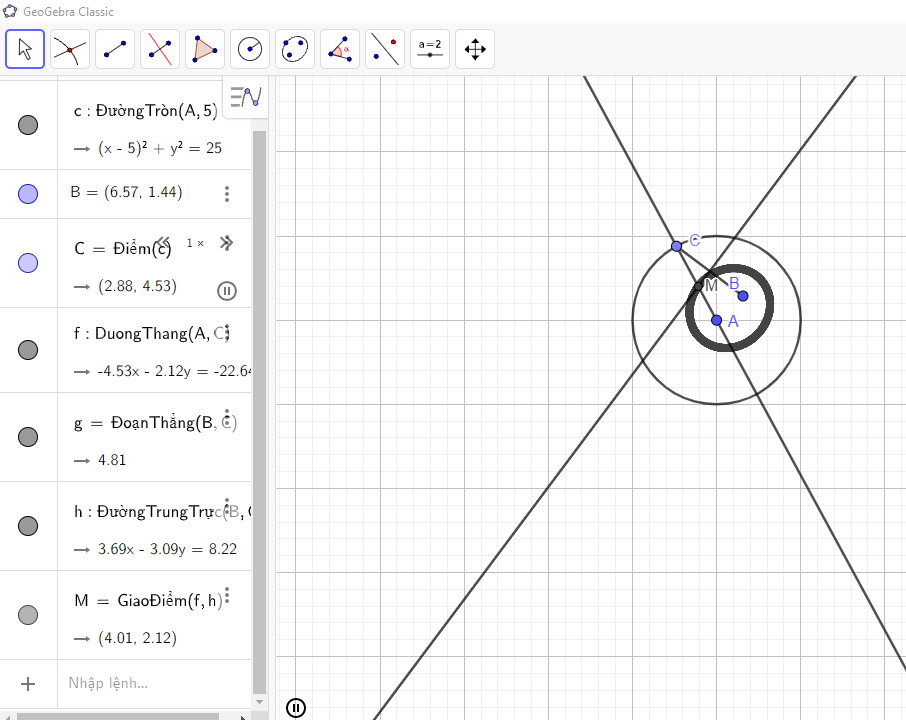
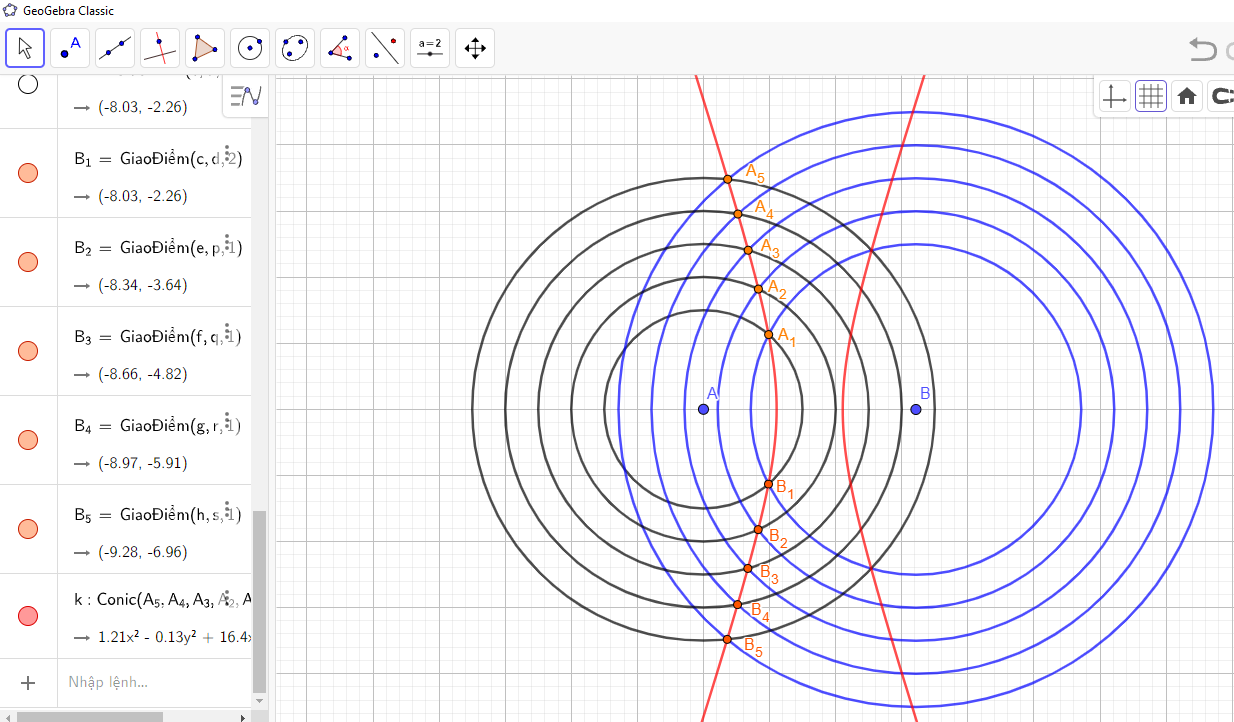
- Vẽ một số đường tròn (ω1), (ω2), (ω3), … có cùng tâm O1 tương ứng có bánh kính R1, R1 + a, R1 + 2a, … và một số đường tròn (Ω1), (Ω2), (Ω3), … có cùng tâm O2, tương ứng có bán kính R2, R2 + a, R2 + 2a, … (R1 ≠ R2). Khi đó, em sẽ quan sát thấy các cặp giao điểm A1, B1; A2, B2; A3, B3; … tương ứng của (ω1) và (Ω1); (ω2) và (Ω2); (ω3) và (Ω3); … là cùng thuộc một nhánh của một hypebol. Kết quả này tương ứng với một hiện tượng vật lí mà em có thể quan sát được: Ném hai hòn sỏi (bằng nhau) xuống mặt hồ lặng sóng, thì em sẽ thấy hai họ đường tròn sóng nước và nói chung giao của chúng tạo nên một đường hypebol.
Chẳng hạn, ta lấy R1 = 3, R2 = 5 và a = 1, ta vẽ được các đường tròn trên như sau: