Câu hỏi:
57 lượt xemLời giải
Hướng dẫn giải:
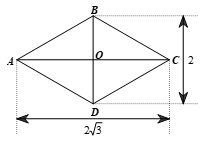
Theo đề ta có hình vẽ:
Hình thoi ABCD có hai đường chéo lần lượt là BD = 2 và AC cắt BD tại O. Khi đó AC ⊥ BD; O là trung điểm của AC, BD.
Suy ra và
Xét ∆OAB vuông tại O, theo định nghĩa tỉ số lượng giác tan, ta có:
suy ra
Theo định lí tổng ba góc của một tam giác, ta có
Suy ra
Hình thoi ABCD có AC, BD là đường chéo nên AC, BD lần lượt là tia phân giác của
Mà (tính chất hình thoi) nên và
Vậy và
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Tự luận
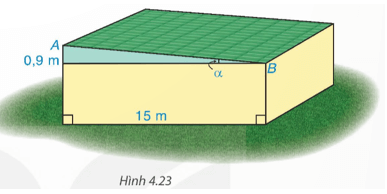
Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.
1 năm trước
236 lượt xem
Câu 16:
Câu 17: