Câu hỏi:
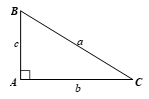
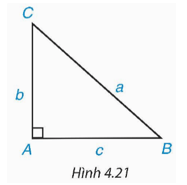
135 lượt xemGiải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:
a) a = 21, b = 18;
b) b = 10,
c) c = 5, b = 3.
Lời giải
Hướng dẫn giải:
a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a2 = b2 + c2
Suy ra (do c > 0).
Theo định nghĩa tỉ số lượng giác sin, ta có Từ đó tìm được
Theo định lí tổng ba góc của một tam giác, ta có
Suy ra
Vậy ∆ABC có
b) Xét ∆ABC vuông tại A, theo định lí tổng ba góc của một tam giác, ta có:
Suy ra
Theo định lí 2, ta có:
Theo định lí 1, ta có AC = b = a.cosC, suy ra
Vậy ∆ABC có
c) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a2 = b2 + c2
Suy ra (vì a > 0).
Theo định nghĩa tỉ số lượng giác tan, ta có suy ra
Theo định lí tổng ba góc của một tam giác, ta có
Suy ra
Vậy ∆ABC có
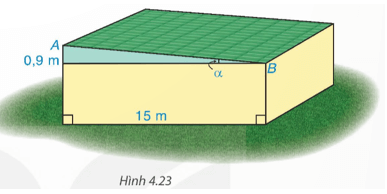
Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.