Câu hỏi:
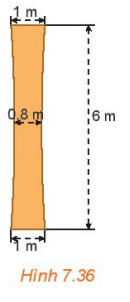
256 lượt xemBài 7.37 trang 59 Toán 10 Tập 2: Một cột trụ hình hyperbol (H.7.36), có chiều cao 6m, chỗ nhỏ nhất ở chính giữa và rộng 0,8m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5m (Tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).
Lời giải
Hướng dẫn giải:
Lời giải
Chọn hệ trục tọa độ Oxy có gốc O là chỗ nhỏ nhất ở chính giữa, như hình vẽ sau:
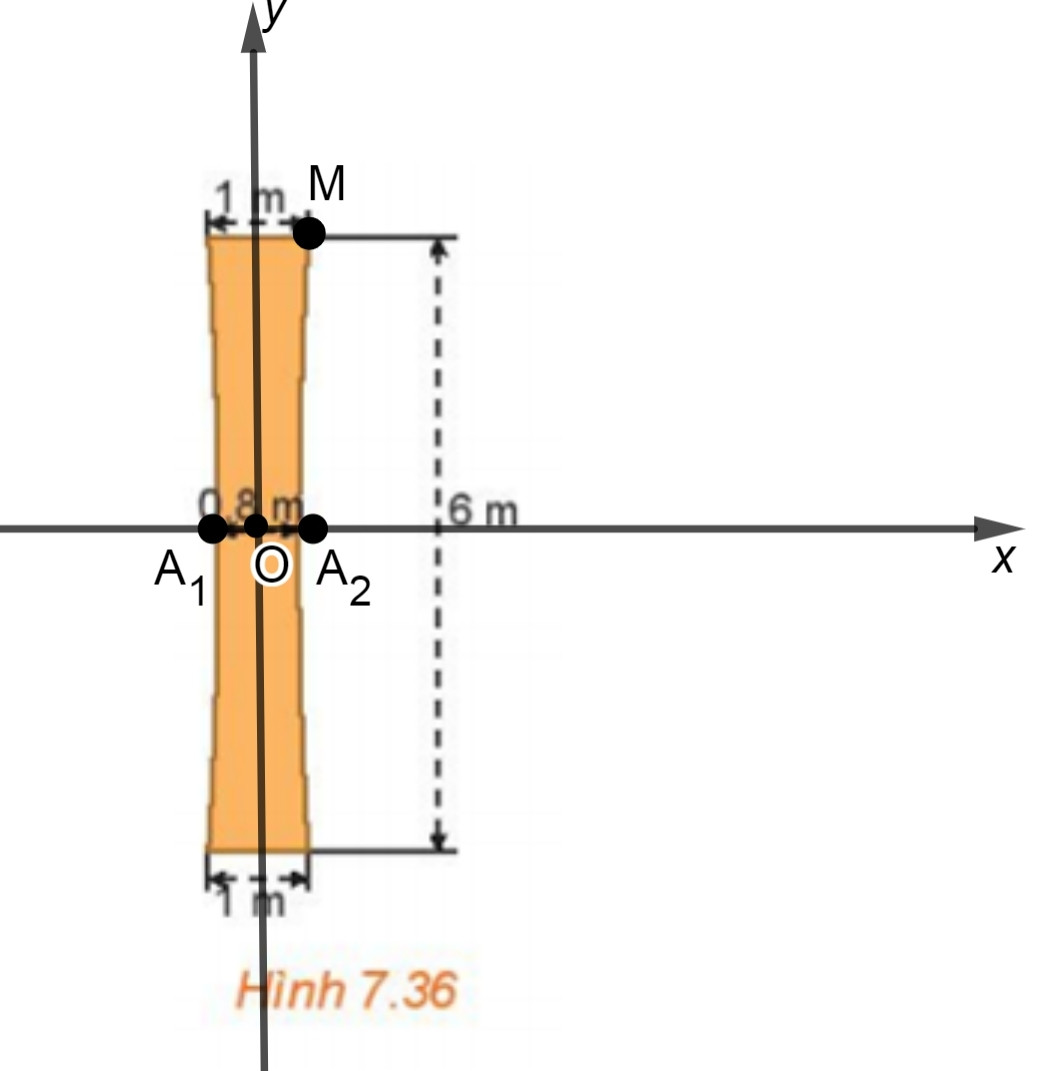
Gọi A1, A2 lần lượt là giao điểm của hypebol với trục hoành mà O là trung điểm của A1A2 nên A1(−0,4 ; 0), A2(0,4 ; 0) hay a = 0,4.
Gọi phương trình hypebol của hình trụ có dạng : .
Gọi M là một điểm trên đỉnh cột nằm ở nhánh bên phải của trục tung hypebol. Ta có toạ độ điểm M(0,5; 3).
Vì điểm M(0,5; 3) thuộc (H) nên
⇔
⇔
⇒ b2 = 16
Do đó phương trình hypebol của hình trụ đó là:
Tại vị trí 5m thì điểm đó cách trục hoành một khoảng bằng 2m nên ta có y = 2.
Thay y = 2 vào phương trình hypebol ta được:
⇔
⇒ x2 = 0,2 ⇒x =≈±0,45
Vậy độ rộng tại vị trí có độ cao 5m xấp xỉ là: 0,45.2 = 0,9 m.