Câu hỏi:
75 lượt xemCho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng
Lời giải
Hướng dẫn giải:
|
GT |
AB = CD, AB // CD; E là giao điểm của AD và BC; ; G, E, H thẳng hàng. |
|
KL |
a) b) EG = EH. |
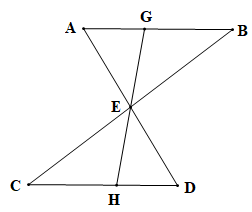
a) Từ AB // CD (theo giả thiết) suy ra (hai góc so le trong) và (hai góc so le trong).
Hay và
Xét tam giác ABE và tam giác DCE có:
(chứng minh trên);
AB = DC (theo giả thiết);
(chứng minh trên).
Vậy (g.c.g).
b) Từ (chứng minh câu a) suy ra AE = DE (hai cạnh tương ứng).
Xét tam giác AEG và tam giác DEH có:
(do );
AE = DE (chứng minh trên);
(hai góc đối đỉnh).
Vậy (g.c.g).
Suy ra EG = EH (hai cạnh tương ứng).
Cho Hình 4.32, biết OA = OD và AB = CD. Chứng minh rằng:
a) AC = DB;
b)
Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho = 80°, = 40° như Hình 4.33
