Câu hỏi:
33 lượt xemCho đường thẳng d và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d. Hai điểm E, F thay đổi trên d sao cho không đổi. Xác định vị trí của hai điểm E, F để AE + BF nhỏ nhất.
Lời giải
Hướng dẫn giải:
Ta có: (m > 0) không đổi.
Đặt , không đổi, khi đó không đổi.
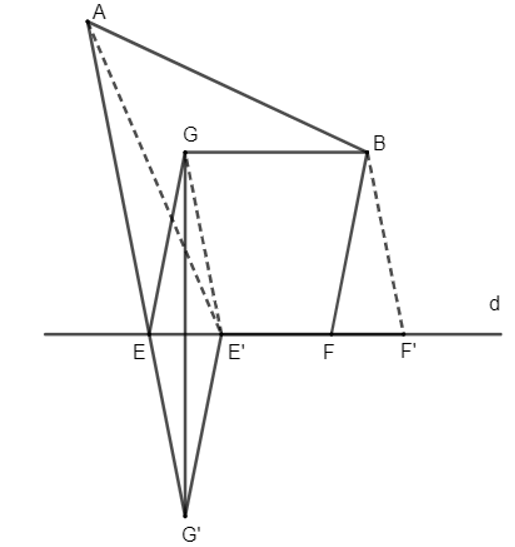
Gọi G là ảnh của điểm B qua phép tịnh tiến theo vectơ . Khi đó . Vì B cố định và không đổi nên G cố định. Gọi G' là ảnh của G qua phép đối xứng trục d thì G' cố định.
Gọi giao điểm của AG' và đường thẳng d là E, trên d lấy điểm F thỏa mãn EF = m và hay . Khi đó BGEF là hình bình hành nên BF = GE.
Mà G và G' đối xứng nhau qua d nên GE = G'E. Do đó BF = GE = G'E.
Ta có: AE + BF = AE + G'E = AG' (1).
Ta có E và F như trên là hai điểm cần tìm để AE + BF nhỏ nhất.
Thật vậy, gọi E' và F' là 2 điểm trên d, khác E và F sao cho và .
Ta có: AE' + BF' = AE' + GE' = AE' + G'E' > AG' (2) (bất đẳng thức trong tam giác AG'E').
Từ (1) và (2) suy ra AE + BF < AE' + BF'. Từ đó suy ra điều phải chứng minh.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 79 lượt thi