Câu hỏi:
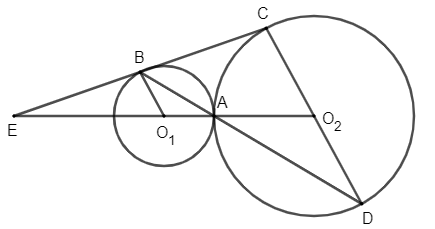
165 lượt xemBài 8 trang 33 Chuyên đề Toán 11: Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Lời giải
Hướng dẫn giải:
Chú ý: Phép vị tự biến đường tròn có bán kính R thành đường tròn có bán kính R' = |k|R và có tâm là ảnh của tâm.
Hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A và đường tròn tâm O2 có bán kính gấp 2 lần đường tròn tâm O1.
- Trên đường tròn (O1; R) lấy điểm B bất kì.
- Trên đường tròn (O2; 2R) dựng đường kính CD // O1B.
- BC cắt O1O2 tại E.
+) Ta có: O1B // CO2 nên theo định lí Thales có .
Suy ra nên ta có phép vị tự tâm E, tỉ số 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm E, tỉ số 2 biến đường tròn (O1; R) thành đường tròn (O2; 2R).
+) Nối B với D, ta chứng minh được BD cắt O1O2 tại điểm tiếp xúc A của hai đường tròn.
Ta có: và A nằm giữa hai điểm O1 và O2 nên . Do đó, ta có phép vị tự tâm A, tỉ số – 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm A, tỉ số – 2 biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Vậy có 2 phép vị tự biến đường tròn (O1; R) thành đường tròn (O2; 2R).