Câu hỏi:
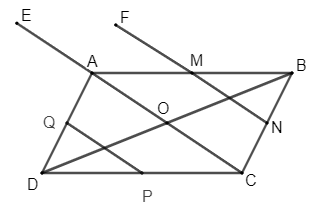
124 lượt xemLuyện tập 1 trang 7 Chuyên đề Toán 11: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ
Lời giải
Hướng dẫn giải:
+ Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = AC. Do đó, (1).
Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC, do đó OA = AC. Suy ra (2).
Từ (1) và (2) suy ra (3).
Vậy ảnh của điểm N qua phép tịnh tiến theo vectơ là điểm M.
+ Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ADC, suy ra PQ // AC và PQ = AC. Do đó, (4)
Từ (2) và (4) suy ra .
Vậy ảnh của điểm P qua phép tịnh tiến theo vectơ là điểm Q.
+ Vì O là trung điểm của AC nên .
Vậy ảnh của điểm C qua phép tịnh tiến theo vectơ là điểm O.
+ Lấy điểm E đối xứng với điểm O qua điểm A, khi đó A là trung điểm của OE.
Suy ra ->.
Vậy ảnh của điểm A qua phép tịnh tiến theo vectơ là điểm E.
+ Lấy điểm F đối xứng với điểm N qua điểm M, khi đó M là trung điểm của NF.
Suy ra (5).
Từ (3) và (5) suy ra .
Vậy ảnh của điểm M qua phép tịnh tiến theo vectơ