Câu hỏi:
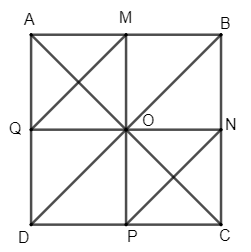
145 lượt xemLuyện tập 3 trang 10 Chuyên đề Toán 11: Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Lời giải
Hướng dẫn giải:
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.