Câu hỏi:
168 lượt xemBài 13 trang 25 Chuyên đề Toán 11: Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.
a) Xác định ảnh của các điểm D và C quay phép quay tâm A với góc quay φ = 60°.
b) Chứng minh rằng DC = BE.
c) Chứng minh rằng số đo góc giữa hai đường thẳng DC và BE bằng 60°.
Lời giải
Hướng dẫn giải:
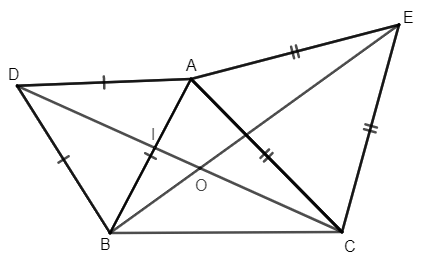
a) + Vì tam giác ABD đều nên AD = AB và .
Phép quay với góc quay φ = 60° có chiều quay ngược chiều kim đồng hồ. Do đó, ảnh của điểm D phép quay tâm A với góc quay φ = 60° là điểm B.
+ Vì tam giác ACE đều nên AC = AE và .
Do đó, ảnh của điểm C phép quay tâm A với góc quay φ = 60° là điểm E.
b) Theo câu a) ta có B và E lần lượt là ảnh của D và C qua phép quay tâm A với góc quay φ = 60°, suy ra DC = BE (phép quay bảo toàn khoảng cách giữa hai điểm bất kì).
c) Gọi O là giao điểm của DC và BE, I là giao điểm của AB và DC.
Ta có phép quay tâm A với góc quay φ = 60° biến góc ADC thành góc ABE nên hay .
Mà (2 góc đối đỉnh), (tổng ba góc trong tam giác ADI) và (tổng ba góc trong tam giác IBO).
Từ đó suy ra hay .
Như vậy, số đo góc giữa hai đường thẳng DC và BE bằng 60°.
