Câu hỏi:

52 lượt xem
Tự luận

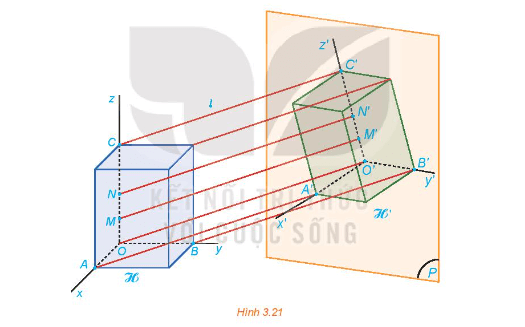
HĐ6 trang 61 Chuyên đề Toán 11: Giả sử hình hộp chữ nhật ℋ trong HĐ5 được gắn thêm các trục Ox, Oy, Oz đôi một vuông góc dọc theo chiều dài, chiều rộng và chiều cao của ℋ. Gọi O'x', O'y' và O'z' lần lượt là hình chiếu của các trục đó lên mặt phẳng (P) theo phương l (H.3.21).

a) Hình chiếu của các góc xOy^,yOz^,zOx^\widehat{xOy},\widehat{yOz},\widehat{zOx}  là các góc nào trên mặt phẳng hình chiếu?

b) Giả sử M, N là hai điểm thuộc trục Oz và M', N' là hình chiếu tương ứng thuộc trục O'z'. So sánh hai tỉ số O′M′OM\dfrac{O'M'}{OM}  và O′N′ON\dfrac{O'N'}{ON} .

HĐ6 trang 61 Chuyên đề Toán 11

Xem đáp án

Xem thêm: Giải chuyên đề Toán 11 (Kết nối tri thức) Bài 11: Hình chiếu vuông góc và hình chiếu trục đo

Lời giải

Hướng dẫn giải:

a) Hình chiếu của các góc \(\widehat{xOy},\widehat{yOz},\widehat{zOx}\) lần lượt là các góc \(\widehat{x'O'y'},\widehat{y'O'z'},\widehat{z'O'x'}\)  trên mặt phẳng hình chiếu.

b) Ta có: OO’ // MM' // NN'.

Suy ra \(\dfrac{O'M'}{O'N'}=\dfrac{OM}{ON}\)  , do đó \(\dfrac{O'M'}{OM}\)  = \(\dfrac{O'N'}{ON}\) .

ĐỀ THI LIÊN QUAN: