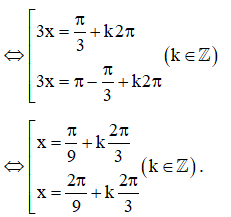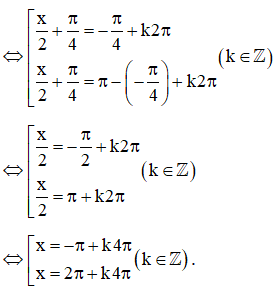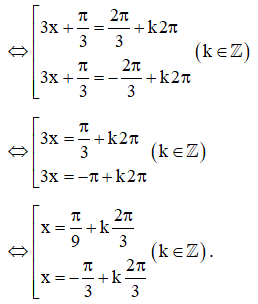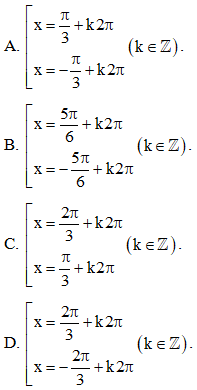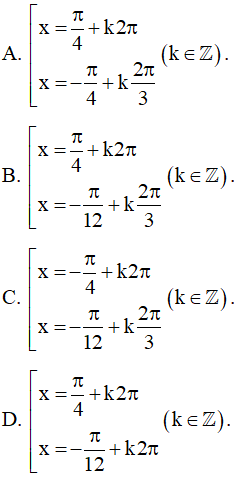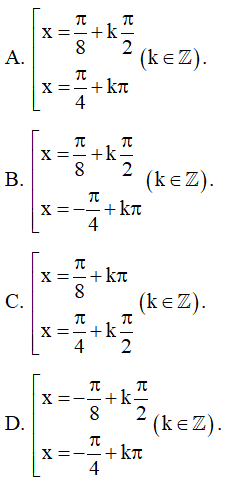Câu hỏi:
94 lượt xemGiải phương trình:
a) sin3x=√32sin3?=32 ;
b) sin(x2+π4)=−√22sin?2+?4=−22 ;
c) cos(3x+π3)=−12cos3?+?3=−12 ;
d) 2cosx+√3=02cos?+3=0 ;
e) √3tanx−1=03tan?−1=0 ;
g) cot(x+π5)=1cot?+?5=1 .
Lời giải
Hướng dẫn giải:
a) Do sinπ3=√32sin?3=32 nên sin3x=√32sin3?=32⇔sin3x=sinπ3⇔sin3?=sin?3
b) Do sin(−π4)=−√22sin−?4=−22 nên sin(x2+π4)=−√22sin?2+?4=−22 ⇔sin(x2+π4)=sin(−π4)⇔sin?2+?4=sin−?4
c) Do cos2π3=−12cos2?3=−12 nên cos(3x+π3)=−12cos3?+?3=−12 ⇔cos(3x+π3)=cos2π3
d) 2cosx+√3=02cos?+3=0
⇔cosx=−√32⇔cos?=−32
⇔cosx=cos5π6⇔cos?=cos5?6 (do cos5π6=−√32cos5?6=−32 )
⇔x=±5π6+k2π(k∈Z)⇔?=±5?6+?2? ?∈ℤ.
e) √3tanx−1=03tan?−1=0
⇔tanx=1√3⇔tan?=13
⇔tanx=tanπ6⇔tan?=tan?6 (do tanπ6=1√3tan?6=13 )
⇔x=π6+kπ(k∈Z)⇔?=?6+?? ?∈ℤ.
g) Do cotπ4=1cot?4=1 nên cot(x+π5)=1cot?+?5=1 ⇔cot(x+π5)=cotπ4⇔cot?+?5=cot?4
⇔x+π5=π4+kπ(k∈Z)⇔?+?5=?4+?? ?∈ℤ
⇔x=π20+kπ(k∈Z)⇔?=?20+?? ?∈ℤ.
Phương trình sin x – cos x = 0 có các nghiệm là:
A. .
B. .
C. .
D. .