Câu hỏi:
468 lượt xemGọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác (OA,OM), (OA,ON), (OA,OP) lần lượt bằng ;;. Chứng minh rằng tam giác MNP là tam giác đều.
Lời giải
Hướng dẫn giải:
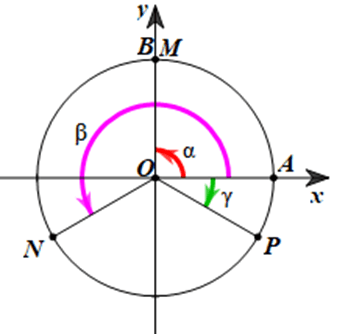
• Ta có (OA,OM) = α = là góc lượng giác có tia đầu là tia OA, tia cuối là tia OM và quay theo chiều dương một góc , khi đó tia OM trùng với tia OB.
Điểm M trên đường tròn lượng giác sao cho (OA,OM) = α = được biểu diễn trùng với điểm B.
• Ta có (OA,ON) = β = = là góc lượng giá.
• Ta có (OA,OP) = = là góc lượng giác có tia đầu là tia OA, tia cuối là tia OP và quay theo chiều âm một góc .
Ba điểm M, N, P trên đường tròn lượng giác được biểu diễn nhu hình vẽ dưới đây:
Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc sau
Đọc tên góc lượng giác, tia đầu và tia cuối của góc lượng giác trong Hình 4b