Câu hỏi:
65 lượt xem Tự luận
HĐ 3 trang 68 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương và .
a) Xác định tọa độ các điểm A và B sao cho
b) Tính AB2, OA2, OB2 theo tọa độ của A và B.
c) Tính theo tọa độ của A, B.
Lời giải
Hướng dẫn giải:
Lời giải
a) Vì mà nên suy ra A(x; y).
Vì mà nên suy ra B(x'; y').
b) +) Ta có: A(x; y) và B(x'; y')
+) Ta có :
+) Ta có:
Vậy và
c) Ta có:
Xét tam giác OAB, theo định lí côsin ta có:
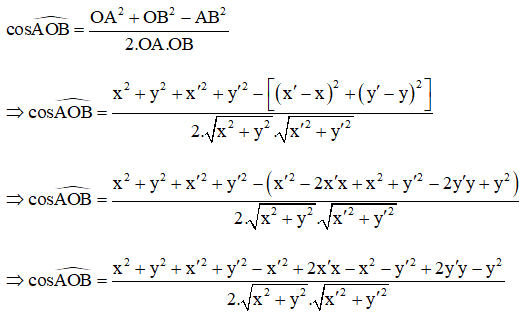
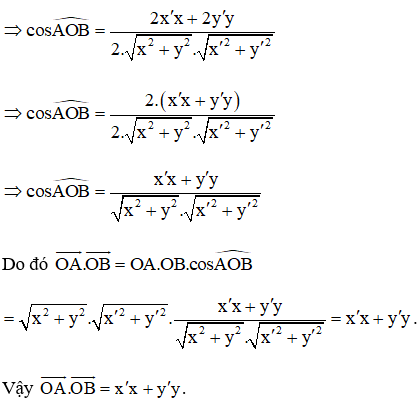
Câu 1: