Lời giải

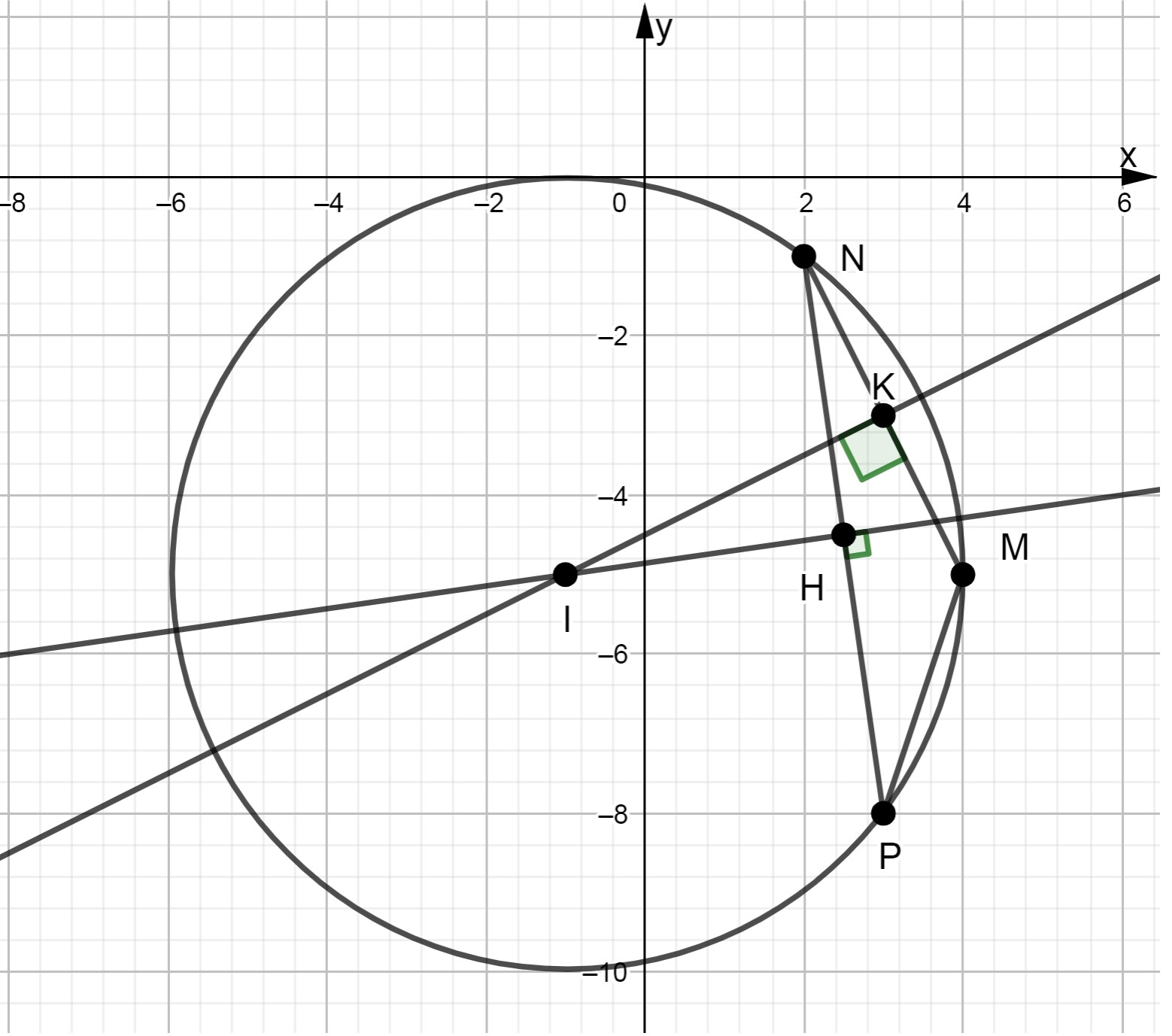
Gọi H và K lần lượt là trung điểm NP và MN

Do đó toạ độ điểm H là $\left\{\begin{array}{l}{x}_H=\frac{2+3}{2}=\frac{5}{2}\\ y_H=\frac{-1-8}{2}=\frac{-9}{2}\end{array}\right.$ ⇒ H$\left(\frac{5}{2};\frac{-9}{2}\right)$

Toạ độ điểm K là $\left\{\begin{array}{l}{x}_K=\frac{2+4}{2}=3\\ y_K=\frac{-5-1}{2}=-3\end{array}\right.$ ⇒ K(3; –3)

Gọi ∆1; ∆2 lần lượt là đường trung trực của NP; MN

Vì đường thẳng ∆1 ⊥ NP nên đường thẳng ∆1 nhận vectơ $\overrightarrow{NP}$ = (1; – 7) làm vectơ pháp tuyến

Phương trình đường thẳng ∆1 đi qua điểm H$\left(\frac{5}{2};\frac{-9}{2}\right)$ và có vectơ pháp tuyến $\overrightarrow{NP}$ là:

$1.\left(x-\frac{5}{2}\right)-7\left(y+\frac{9}{2}\right)=0$ hay x – 7y – 34 = 0

Tương tự ta có đường thẳng ∆2 nhận vectơ $\overrightarrow{MN}$ = (–2; 4) làm vectơ pháp tuyến

Phương trình đường thẳng ∆2 đi qua điểm K(3; –3) và có vectơ pháp tuyến $\overrightarrow{MN}$ là:

–2.(x – 3) + 4.(y + 3) = 0 ⇔ –2x + 4y + 18 = 0 hay –x + 2y + 9 = 0.

Gọi I là giao điểm của hai đường thẳng ∆1; ∆2. Do đó ,toạ độ điểm I thoả mãn hệ phương trình : $\left\{\begin{array}{l}x-7y-34=0\\ -x+2y+9=0\end{array}\right.$

Cộng hai phương trình trong hệ trên vế theo vế ta được: –5y – 25 = 0 ⇒ y = –5

Thay y = –5 vào phương trình –x + 2y + 9 = 0 ta được : –x + 2(–5) + 9 = 0

                                        ⇒ –x – 1 = 0 ⇒  x = –1

Suy ra tâm I của đường tròn đi qua ba điểm M, N, P là I (–1; –5) và bán kính

R = IM = $\sqrt{5^2+0^2}=5$

Vậy phương trình đường tròn (C) là: (x +1)2 + (y + 5)2 = 25.