Lời giải

a) Vì H là trực tâm của tam giác ABC nên:

+) $AH\perp BC\Rightarrow \overrightarrow{AH}\perp \overrightarrow{BC}\Rightarrow \overrightarrow{AH}.\overrightarrow{BC}=0;$

+) $BH\perp CA\Rightarrow \overrightarrow{BH}\perp \overrightarrow{CA}\Rightarrow \overrightarrow{BH}.\overrightarrow{CA}=0$.

Vậy $\overrightarrow{AH}.\overrightarrow{BC}=0$ và $\overrightarrow{BH}.\overrightarrow{CA}=0$.

b) Gọi tọa độ điểm H là H(x; y).

Ta có: A(‒1;2), B(8;‒1), C(8;8) và H(x; y).

$\Rightarrow \overrightarrow{AH}=\left(x+1;y-2\right);\overrightarrow{BC}=\left(0;9\right)$ và $\overrightarrow{BH}=\left(x-8;y+1\right);\overrightarrow{AC}=\left(9;6\right)$

Suy ra $\overrightarrow{AH}.\overrightarrow{BC}=\left(x+1\right).0+\left(y-2\right).9=9\left(y-2\right).$

Và $\overrightarrow{BH}.\overrightarrow{AC}=\left(x-8\right).9+\left(y+1\right).6=9x-72+6y+6=9x+6y-66$.

Theo câu a ta có: $\overrightarrow{AH}.\overrightarrow{BC}=0$$\iff$ 9(y – 2) = 0 $\iff$ y – 2 = 0 $\iff$ y = 2.

Và  $\overrightarrow{BH}.\overrightarrow{AC}=0$ (do BH ⊥ AC)$\iff$ 9x + 6y – 66 = 0.

Thay y = 2 vào 9x + 6y – 66 = 0 ta được: 9x + 6.2 – 66 = 0

$\iff$ 9x – 54 = 0

$\iff$ 9x = 54

$\iff$ x = 6

⇒ H(6; 2)

Vậy H(6; 2).

c) Với A(‒1;2), B(8;‒1), C(8;8) ta có:

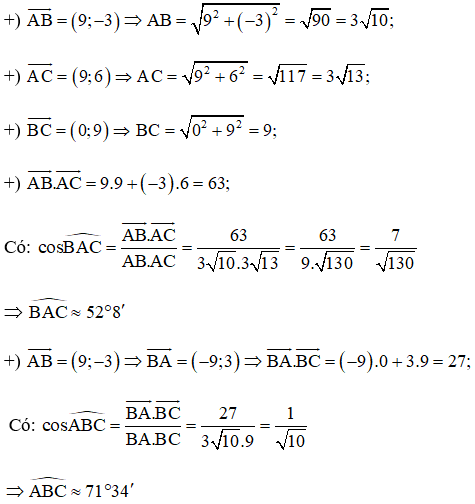
Xét tam giác ABC, theo định lí tổng ba góc trong một tam giác ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$

$\Rightarrow \widehat{ACB}=180°-\left(\widehat{BAC}+\widehat{ABC}\right)$  

$\Rightarrow \widehat{ACB}\approx 180°-\left(52°8^{\text{'}}+71°{34}^{\text{'}}\right)\approx 56°{18}^{\text{'}}$

Vậy 

$$\begin{gathered} AB=3\sqrt{10},AC=3\sqrt{13},BC=9,\widehat{BAC} \\ \approx 52°8^{\text{'}},\widehat{ABC}\approx 71°{34}^{\text{'}},\widehat{ACB}\approx 56°{18}^{\text{'}}. \end{gathered}$$