Câu hỏi:
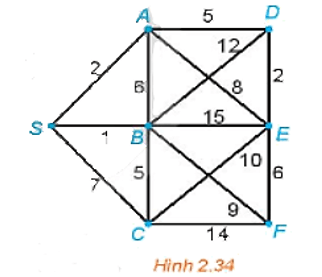
245 lượt xemBài 2.16 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh S đến mỗi đỉnh khác của đồ thị có trọng số trên Hình 2.34.
Lời giải
Hướng dẫn giải:
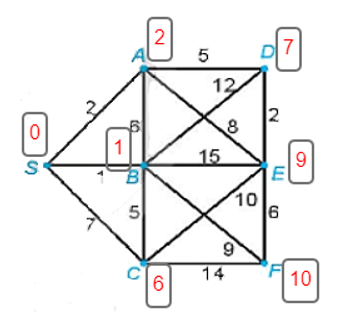
Đầu tiên ta gắn nhãn đỉnh S là I(S) = 0 và gắn cho ba đỉnh kề với S là A, B và C các nhãn tạm thời là I(S) + 2, I(S) + 1 và I(S) + 7. Chọn số nhỏ nhất trong chúng và viết I(B) = 1. Đỉnh B bây giờ được gắn nhãn vĩnh viễn là 1.
Tiếp theo ta gắn nhãn cho các đỉnh kề với B là A, C, D, E và F các nhãn tạm thời là I(B) + 6 (hiện A có 2 nhãn tạm thời là 2 và 7), I(B) + 5 (hiện C có hai nhãn tạm thời là 7 và 6), I(B) + 12, I(B) + 15, I(B) + 9. Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (tại A, C, D, E, F) hiện nay là 2 (tại A), nên ta viết I(A) = 2. Điểm A được gắn nhãn vĩnh viễn là 2.
Bây giờ ta xét các đỉnh kề với A mà chưa được gắn nhãn vĩnh viễn là D và E. Ta gắn cho đỉnh D nhãn tạm thời I(A) + 5 (hiện D có hai nhãn tạm thời là 13 và 7), gắn cho đỉnh E nhãn tạm thời I(A) + 8 (hiện E có hai nhãn tạm thời là 16 và 10). Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (tại D và E) là 7 (tại D), nên ta viết I(D) = 7. Đỉnh D được gắn nhãn vĩnh viễn là 7.
Ta xét đỉnh E (chưa được gắn nhãn vĩnh viễn) kề với D, ta gắn nhãn tạm thời I(D) + 2 (hiện E có ba nhãn tạm thời là 16, 10 và 9). Vậy đỉnh E sẽ được gắn nhãn vĩnh viễn là 9 hay I(E) = 9.
Tiếp tục ta xét các đỉnh kề với E mà chưa được gắn nhãn vĩnh viễn là C và F. Ta gắn cho đỉnh C nhãn tạm thời I(E) + 10 (hiện C có ba nhãn tạm thời là 7, 6 và 19), gắn cho F nhãn tạm thời I(E) + 6 (hiện F có hai nhãn tạm thời là 10 và 15). Nhãn tạm thời nhỏ nhất trong các nhãn đã gắn (ở C, F) hiện nay là 6 (tại C), nên ta viết I(C) = 6. Đỉnh C được gắn nhãn vĩnh viễn là 6.
Xét đỉnh kề với C là F, ta gắn cho F nhãn tạm thời I(C) + 14 (hiện F có ba nhãn tạm thời là 10, 15 và 20) nên I(F) = 10. Đỉnh F được gắn nhãn vĩnh viễn là 10.
Vậy, đường đi ngắn nhất từ đỉnh S đến đỉnh A là SA = 2.
Đường đi ngắn nhất từ đỉnh S đến đỉnh B là SB = 1.
Đường đi ngắn nhất từ đỉnh S đến đỉnh C có độ dài là I(C) = 6 và có đường đi là
S → B → C.
Đường đi ngắn nhất từ đỉnh S đến đỉnh D có độ dài là I(D) = 7 và đường đi là
S → A → D.
Đường đi ngắn nhất từ đỉnh S đến đỉnh E có độ dài là I(E) = 9 và đường đi là
S → A → D → E.
Đường đi ngắn nhất từ đỉnh S đến đỉnh F có độ dài là I(F) = 10 và đường đi là
S → B → F.