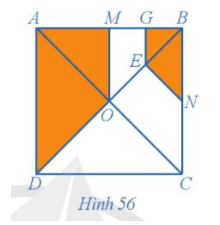
+) Vì O là giao hai đường chéo của hình vuông ABCD nên AC và BD vuông góc với nhau tại O và O là trung điểm của AC và BD, lại có AC = BD nên suy ra OA = OB = OC = OD.

Tam giác OBC cân tại O (OB = OC) có ON là đường trung tuyến nên ON là đường phân giác, suy ra $\widehat{CON}=\widehat{BON}=\frac{\widehat{BOC}}{2}=\frac{90°}{2}=45°$.

Tương tự ta chứng minh được $\widehat{BOM}=45°$  hay $\widehat{EOM}=45°$ .

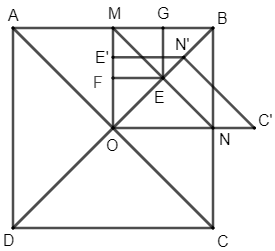
Trên tia ON, lấy điểm C' sao cho OC' = OC. Trên tia OB, lấy điểm N' sao cho ON' = ON. Trên tia OM, lấy điểm E' sao cho OE' = OE.

Lại có $\widehat{COC\text{'}}=\widehat{CON}=45°$ , $\widehat{NON\text{'}}=\widehat{BON}=45°$ và $\widehat{NON\text{'}}=\widehat{BON}=45°$.

Mà phép quay với góc quay 45° có chiều quay ngược chiều kim đồng hồ.

Do đó, ta có phép quay tâm O với góc quay 45° biến các điểm C, O, E, N tương ứng thành các điểm C'¸O, E', N' nên phép quay tâm O với góc quay 45° biến hình COEN thành hình C'OE'N' (1).

+) Giả sử hình vuông ABCD có cạnh là a.

Khi đó BD = AC = a$\sqrt{2}$, OB = OC = $\frac{a\sqrt{2}}{2}$, ON = $\frac{AB}{2}=\frac{a}{2}$ .

Suy ra $OE=\frac{OB}{2}=\frac{a\sqrt{2}}{4}$, OC' = OC = $\frac{a\sqrt{2}}{2}$, ON' = ON = $\frac{a}{2}$.

Suy ra $\frac{OE}{ON\text{'}}=\frac{\sqrt{2}}{2},\frac{ON}{OC\text{'}}=\frac{\sqrt{2}}{2}$, do đó $\frac{OE}{ON\text{'}}=\frac{ON}{OC\text{'}}=\frac{\sqrt{2}}{2}$.

Qua E, kẻ đường thẳng song song với E'N' cắt OM tại F, suy ra EF // E'N' nên theo định lí Thales trong tam giác OE'N' ta có $\frac{OF}{OE\text{'}}=\frac{OE}{ON\text{'}}=\frac{\sqrt{2}}{2}$.  

Từ đó suy ra $\frac{ON}{OC\text{'}}=\frac{OE}{ON\text{'}}=\frac{OF}{OE\text{'}}=\frac{\sqrt{2}}{2}$ nên $\overrightarrow{ON}=\frac{\sqrt{2}}{2}\overrightarrow{OC\text{'}}$, $\overrightarrow{OE}=\frac{\sqrt{2}}{2}\overrightarrow{ON\text{'}}$, $\overrightarrow{OF}=\frac{\sqrt{2}}{2}\overrightarrow{OE\text{'}}$ .

Như vậy, ta có phép vị tự tâm O với tỉ số $\frac{\sqrt{2}}{2}$biến các điểm C'¸O, E', N' tương ứng thành các điểm N, O, F, E hay phép vị tự tâm O với tỉ số $\frac{\sqrt{2}}{2}$ biến hình C'OE'N' thành hình NOFE (2).

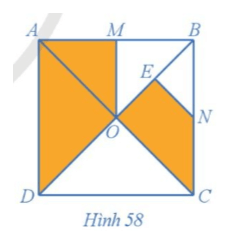
+)  Tam giác NOB vuông cân tại N có NE là đường trung tuyến nên NE cũng là đường cao và NE = $\frac{OB}{2}$ = OE, suy ra $\widehat{NEO}=90°$  và EN = EO.

Tương tự, ta chứng minh được $\widehat{MEO}=90°$và EM = EO.

Ta chứng minh được EFMG là hình vuông nên $\widehat{FEG}=90°$ và EF = EG.

Mà phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.

Do đó, ta có phép quay tâm E với góc quay – 90° biến các điểm N, O, F, E tương ứng thành các điểm O, M, G, E hay phép quay tâm E với góc quay – 90° biến hình NOFE thành hình OMGE (3).

Từ (1), (2) và (3) suy ra hai hình OMGE và COEN đồng dạng với nhau.