10 Đề thi Toán 11 Giữa học kì 1 Cánh diều (2024 có đáp án)

Chỉ từ 150k mua trọn bộ Đề thi Toán 11 Giữa học kì 1 Cánh diều bản word có lời giải chi tiết (Chỉ 25k cho 1 đề thi bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Giữa Học kì 1 Toán lớp 11 (Cánh diều) 2024 có đáp án

Sở Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Năm học ...

Môn: Toán lớp 11

Thời gian làm bài: phút

Đề thi Giữa Học kì 1 Toán 11 Cánh diều (Đề số 1)

Phần trắc nghiệm (5 điểm)

Câu 1: Cho góc lượng giác (Ov, Ow) có số đo là $\frac{4\pi }{5}$, góc lượng giác (Ou, Ow) có số đo là $\frac{7\pi }{5}$. Số đo góc lượng giác (Ou, Ov) là:

A. $\frac{\pi }{5}+k2\pi \left(k\in \mathbb{Z}\right)$

B. $\frac{3\pi }{5}+k2\pi \left(k\in \mathbb{Z}\right)$

C. $\frac{-\pi }{5}+k2\pi \left(k\in \mathbb{Z}\right)$

D. Cả A, B, C đều sai

Câu 2: Cho $\cos x=\frac{-1}{3}$ với $\frac{\pi }{2}<x<\pi$. Chọn đáp án đúng:

Câu 3: Cho $\sin \alpha +\cos \alpha =\frac{1}{4}$. Khi đó:

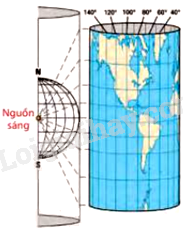
Câu 5: Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong hình vẽ. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến $0^0$ làm trục tung. Khi đó tung độ của một điểm có vĩ độ ${\phi }^0\left(-90<\phi <90\right)$ được cho bởi hàm số $y=20\tan \left(\frac{\pi }{180}\phi \right)\left(cm\right)$. Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo không quá 20cm trên bản đồ.

Câu 6: Sử dụng máy tính cầm tay để giải phương trình $\tan x-6=0$ với kết quả là radian (làm tròn kết quả đến hàng phần nghìn) là:

Câu 7: Có bao nhiêu số nguyên m sao cho phương trình $2{\sin }^{2}x-\sin x\cos x-{\cos }^{2}x=m$ có nghiệm?

A. 1	B. 2
C. 3	D. 4

Câu 8: Cho dãy số có các số hạng đầu là: $\frac{1}{4};\frac{1}{4^2};\frac{1}{4^3};\frac{1}{4^4};\frac{1}{4^5};...$ Số hạng tổng quát của dãy số này là:

A. $u_n=\frac{1}{4^{n+2}}$	B. $u_n=\frac{1}{4^{n+1}}$
C. $u_n=\frac{1}{4^n}$	D. $u_n=\frac{1}{4^{n-1}}$

Câu 9: Cho dãy số $\left(u_n\right)$ với $u_n=\frac{na+3}{n+1}$. Với giá trị nào của a thì $\left(u_n\right)$ là dãy số tăng:

A. $a=3$	B. $a<3$
C.  $a<4$	D. $a>3$

Câu 10: Trong các dãy số sau, dãy nào không là cấp số cộng?

A. $3;1;-1;-3;-5$	B. $5;2;-1;-4;-7$
C. $2;4;6;8;10$	D. $1;2;3;5;8$

Câu 11: Cho cấp số cộng có $u_2=2017,u_5=1945$. Số hạng tổng quát của cấp số cộng này là:

A. $u_n=-24n+2065$	B. $u_n=24n-2065$
C. $u_n=-12n+2065$	D. $u_n=12n-2065$

Câu 12: Sinh nhật lần thứ 20 của An vào ngày 01 tháng 5 năm 2018 dương lịch. An muốn mua một món quà để làm quà sinh nhật cho chính mình nên An quyết định nuôi lợn đất. An bắt đầu bỏ vào lợn 1 000 đồng vào ngày 01 tháng 02 năm 2018. Trong các ngày tiếp theo, ngày sau An bỏ tiền vào lợn đất nhiều hơn ngày trước đó 2000 đồng. Hỏi đến ngày sinh nhật mình, An có bao nhiêu tiền để mua quà (ngày nuôi lợn đất tình từ ngày 01 tháng 02 năm 2018 đến hết ngày 30 tháng 04 năm 2018)?

A. 7 925 000 đồng	B. 7 921 000 đồng
C.  7 920 000 đồng	D. 6 920 000 đồng

Câu 13: Dãy số $\left(u_n\right)$ nào sau đây là dãy số giảm?

A. $1;2;3;4;5;...$	B. $1;-1;2;-2;...$
C. $-1;-2;-3;-4;-5;...$	D. Cả A, B, C đều sai

Câu 14: Hình chóp tứ giác thì có mặt bên là hình gì?

A. Hình tam giác	B. Hình tứ giác
C. Hình ngũ giác	D. Cả A, B, C đều sai

Câu 15: Với ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và cùng đi qua một điểm O, ta xác định được bao nhiêu mặt phẳng?

A. 1 mặt phẳng	B. 2 mặt phẳng
C. 3 mặt phẳng	D. 4 mặt phẳng

Câu 16: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Gọi P là điểm thuộc cạnh AD sao cho $AP=2DP$. Giao tuyến của hai mặt phẳng (MNP) và (BCD) là:

Câu 17: Hai đường thẳng nằm trong cùng một mặt phẳng và không có điểm chung thì hai đường thẳng đó:

A. Chéo nhau	B. Song song
C. Cắt nhau	D. Trùng nhau

Câu 18: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo hình bình hành ABCD và ABEF. Khẳng định nào dưới đây đúng?

Câu 19: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, BC, AD. I là giao điểm của MN và PQ. Khẳng định nào sau đây đúng?

A. $MI=\frac{2}{3}MN$	B. $MI=\frac{1}{3}MN$
C. $MI=\frac{2}{3}MN$	D. $MI=\frac{1}{2}MN$

Câu 20: Cho tam giác ABC cân tại A. Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB theo thứ tự lập thành cấp số nhân với công bội q. Khẳng định nào dưới đây đúng?

A. $q^2=\frac{\sqrt{2}+1}{2}$	B. $q^2=\frac{2\sqrt{2}-1}{2}$
C. $q^2=\frac{\sqrt{2}+1}{4}$	D. $q^2=\frac{2\sqrt{2}-1}{4}$

Phần tự luận (5 điểm)

Bài 1. (1,5 điểm)

1) Giải các phương trình sau:

a) $\cot \left(\frac{1}{2}x+\frac{\pi }{4}\right)=1$

b) $\sin x+\sin 2x=0$

2) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=1+2{\sin }^{2}x-3{\cos }^{2}x$

3) Cho phương trình: $\left(1-m\right){\tan }^{2}x-\frac{2}{\cos x}+1+3m=0$. Tìm m để phương trình có nhiều hơn một nghiệm trên $\left(0;\frac{\pi }{2}\right)$.

Bài 2. (1,5 điểm)

a) Cho cấp số cộng $\left(u_n\right)$ với $u_1=\frac{1}{3}$ và $u_1+u_2+u_3=-1$. Tìm công thức số hạng tổng quát $u_n$ của cấp số cộng đó.

b) Cho dãy số có các số hạng đầu là 4; 8; 12; 16; 20; 24;… Tìm số hạng tổng quát của dãy số đó.

Bài 3. (1,0 điểm) Cho hình chóp S. ABCD. Gọi O là một điểm nằm trong tam giác SCD. Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Bài 4. (1,0 điểm) Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.

a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.

b) Chứng minh rằng các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.

Sở Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Năm học ...

Môn: Toán lớp 11

Thời gian làm bài: phút

Đề thi Giữa Học kì 1 Toán 11 Cánh diều (Đề số 2)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Nếu một góc lượng giác có số đo là $\alpha =-{45}^{\text{o}}$ thì số đo radian của nó là

A. $-\frac{\pi }{2}$;

B. $-\frac{\pi }{4}$;

C. $\frac{\pi }{4}$;

D. $\frac{\pi }{2}$.

Câu 2. Điểm cuối của góc lượng giác $\alpha$ở góc phần tư thứ mấy nếu $\text{sin}\alpha ,\text{cos}\alpha$cùng dấu?

A. Thứ II;

B. Thứ IV;

C. Thứ II hoặc IV;

D. Thứ I hoặc III.

Câu 3. Cho góc lượng giác $\left(Ou,Ov\right)$ có số đo là $\frac{\pi }{4}$. Số đo của các góc lượng giác nào sau đây có cùng tia đầu là $Ou$và tia cuối là $Ov$?

A. $\frac{3\pi }{4}$;

B. $\frac{5\pi }{4}$;

C. $\frac{7\pi }{4}$;

D. $\frac{9\pi }{4}$.

Câu 4. Cho $\text{cos}\alpha =\frac{1}{3}$. Khi đó $\text{sin}\left(\alpha -\frac{3\pi }{2}\right)$bằng

A. $-\frac{2}{3}$;

B. $-\frac{1}{3}$;

C. $\frac{1}{3}$;

D. $\frac{2}{3}$.

Câu 5. Cho góc $\alpha$thỏa mãn $\text{sin}\alpha +\text{cos}\alpha =\frac{5}{4}$. Giá trị của $P=\text{sin}\alpha .\text{cos}\alpha$là

A. $P=\frac{9}{16}$;

B. $P=\frac{9}{32}$;

C. $P=\frac{9}{8}$;

D. $P=\frac{1}{8}$.

Câu 6. Rút gọn biểu thức $M=\sin \left(x-y\right)\cos y+\cos \left(x-y\right)\sin y$ta được

A. $M=\cos x$;

B. $M=\sin x$;

C. $M=\sin x\cos 2y$;

D. $M=\cos x\cos 2y$

Câu 7. Khẳng định nào sau đây là sai?

A. Hàm số $y=\sin x$là hàm số lẻ;

B. Hàm số $y=\cos x$là hàm số lẻ;

C. Hàm số $y=\tan x$là hàm số lẻ;

D. Hàm số $y=\cot x$là hàm số lẻ.

Câu 8. Hàm số $y=f\left(x\right)$có tập xác định $D$là hàm số tuần hoàn nếu tồn tại một số $T$khác 0sao cho $\forall x\in D$ta có $x+T\in D,x-T\in D$và

A. $f\left(x+T\right)=f\left(x\right)$;

B. $f\left(x+T\right)=-f\left(x\right)$;

C. $f\left(x+T\right)=2\pi f\left(x\right)$;

D. $f\left(x+T\right)=-2\pi f\left(x\right)$.

Câu 9. Cho hàm số $y=\sin x$có đồ thị như hình vẽ dưới đây:

Hàm số $y=\sin x$ nghịch biến trên khoảng nào?

A. $\left(0;\pi \right)$;

B. $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$;

C. $\left(-2\pi ;-\pi \right)$;

D. $\left(-\frac{5\pi }{2};-\frac{3\pi }{2}\right)$.

Câu 10. Tập xác định D của hàm số $y=\frac{1}{\sqrt{1-\text{sin}x}}$ là

A. $D=ℝ\backslash \left(k\pi ,k\in \mathbb{Z}\right)$;

B. $D=ℝ\backslash \left(\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)$;

C. $D=ℝ\backslash \left(\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\right)$;

D. $D=\varnothing$.

Câu 11. Giá trị lớn nhất $M$ của hàm số $y=1-2\left(\text{cos}3x\right)$là

A. M = 3;

B. M = 2;

C. M = 1;

D. M = 0.

Câu 12. Công thức nghiệm $x=\alpha +k\pi$ với $k\in \mathbb{Z}$ là công thức nghiệm của phương trình nào sau đây?

A. $\tan x=\tan {\alpha }^{\text{o}}$;

B. $\sin x=\sin \alpha$;

C. $\cos x=\cos \alpha$;

D. $\tan x=\tan \alpha$

Câu 13. Nghiệm đặc biệt nào sau đây là sai?

A. $\cos x=0\iff x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$;

B. $\sin x=0\iff x=k\pi \left(k\in \mathbb{Z}\right)$;

C. $\sin x=1\iff x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$;

D. $\sin x=-1\iff x=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$.

Câu 14. Các giá trị của tham số mđể phương trình $\cos x=-m$vô nghiệm là

A. $m\in \left(-\infty ;-1\right)\cup \left(1;+\infty \right)$;

B. $m\in \left(1;+\infty \right)$;

C. $m\in \left(-1;1\right)$;

D.$m\in \left(-\infty ;-1\right)$.

Câu 15. Nghiệm của phương trình $\cot \left(\frac{x}{2}+\frac{\pi }{4}\right)=-1$ là

A. $x=-\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$;

B. $x=-\pi +k\pi ,k\in \mathbb{Z}$;

C. $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$;

D. $x=-\pi +k2\pi ,k\in \mathbb{Z}$.

Câu 16. Với $n\in {\mathbb{N}}^{*}$, cho dãy số $\left(u_n\right)$có số hạng tổng quát $u_n=n^2-1$. Năm số hạng đầu tiên của dãy số này là

A. $-1;0;3;8;16$;

B. $1;4;9;16;25$;

C. $0;3;8;15;24$;

D. $0;3;6;9;12$.

Câu 17. Với $n\in {\mathbb{N}}^{*}$, cho dãy số $\left(u_n\right)$gồm các số nguyên dương chia hết cho 7 là 7,14, 21, … Công thức số hạng tổng quát của dãy số này là

A. $u_n=7n-7$;

B. $u_n=7n+7$;

C. $u_n=7n$;

D. $u_n=7n^2$.

Câu 18. Cho dãy số $\left(u_n\right)$biết $u_n=\frac{3n-1}{3n+1}$. Dãy số $\left(u_n\right)$ bị chặn trên bởi số nào dưới đây?

A. 0;

B. $\frac{1}{2}$;

C. $\frac{1}{3}$;

D. 1.

Câu 19. Cho cấp số cộng $\left(u_n\right),$ có số hạng đầu bằng $u_1$ và công sai bằng $d.$ Công thức số hạng tổng quát $u_n$là

A. $u_n=u_1+nd$;

B. $u_n=u_1+\left(n-1\right)d$;

C. $u_n=u_1+\left(n+1\right)d$;

D. $u_n=u_1+\left(1-n\right)d$.

Câu 20. Cho dãy số $\frac{1}{2};0;-\frac{1}{2};-1;\frac{-3}{2};\mathrm{...}$là cấp số cộng với

A. số hạng đầu tiên là $\frac{1}{2}$và công sai là $\frac{1}{2}$;

B. số hạng đầu tiên là $\frac{1}{2}$và công sai là $-\frac{1}{2}$;

C. số hạng đầu tiên là 0 và công sai là $\frac{1}{2}$;

D. số hạng đầu tiên là 0 và công sai là $-\frac{1}{2}$.

Câu 21. Tổng của bao nhiêu số hạng đầu của cấp số cộng $1;-1;-3;\mathrm{...}$ bằng $-9800$ ?

A. 98;

B. 99;

C. 100;

D. 101.

Câu 22. Cho hai đường thẳng avà chéo nhau. Có bao nhiêu mặt phẳng chứa avà song song với ?

A. 0;

B. 1;

C. 2;

D. vô số.

Câu 23. Cho hình chóp $S.ABCD$(hình vẽ). Gọi O là giao điểm của AC và BD. Điểm Okhông thuộc mặt phẳng nào sau đây?

A. $\left(SAC\right)$;

B. $\left(SBD\right)$;

C. $\left(SAB\right)$;

D. $\left(ABCD\right)$.

Câu 24. Hình chóp lục giác có bao nhiêu mặt bên?

A. 4;

B. 5;

C. 6;

D. 7.

Câu 25. Khẳng định nào sau đây là đúng về hình tứ diện đều?

A. Mặt đáy là hình thoi;

B. Mặt đáy là hình vuông;

C. Mặt bên là tam giác cân;

D. Mặt bên luôn là tam giác đều.

Câu 26. Cho hình chóp A.BCD có là trọng tâm tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là

A. AN với N là trung điểm của CD;

B. AM với Mlà trung điểm của AB;

C. AH với Hlà hình chiếu của B trên CD;

D. AK với là hình chiếu của C trên .

Câu 27. Cho tứ diện ABCD có M, lần lượt là trung điểm của BC, . Gọi Glà trọng tâm của tam giác BCD. Gọi Ilà giao điểm của NGvới mặt phẳng (ABC). Khẳng định nào sau đây đúng?

A. $I\in AM$;

B. $I\in BC$;

C. $I\in AC$;

D. $I\in AB$

Câu 28. Cho ba mặt phẳng phân biệt $\left(\alpha \right),\left(\beta \right),\left(\gamma \right)$có $\left(\alpha \right)\cap \left(\beta \right)=a$, $\left(\beta \right)\cap \left(\gamma \right)=b$, $\left(\alpha \right)\cap \left(\gamma \right)=c$. Khi đó ba đường thẳng $a,b,c$sẽ

A. đôi một cắt nhau;

B. đôi một song song;

C. đồng quy;

D. đôi một song song hoặc đồng quy.

Câu 29. Trong không gian, cho ba đường thẳng $a,b,c$biết $a\text{//}b$và a, c chéo nhau. Khi đó hai đường thẳng b và csẽ

A. trùng nhau hoặc chéo nhau;

B. cắt nhau hoặc chéo nhau;

C. chéo nhau hoặc song song;

D. song song hoặc trùng nhau.

Câu 30. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Khẳng định nào sau đây là đúng?

A. IJ song song với CD;

B. IJ song song với AB;

C. IJ chéo CD;

D. IJ cắt AB.

Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây đúng?

A. MN và SD cắt nhau;

B. MN // CD;

C. MN và SC cắt nhau;

D. MN và CD chéo nhau.

Câu 32. Cho đường thẳng asong song với mặt phẳng $\left(\alpha \right)$. Nếu mặt phẳng $\left(\beta \right)$ chứa a và cắt $\left(\alpha \right)$ theo giao tuyến b thì b và a là hai đường thẳng

A. cắt nhau;

B. trùng nhau;

C. chéo nhau;

D. song song với nhau.

Câu 33. Cho các giả thiết sau. Giả thiết nào kết luận đường thẳng asong song với mặt phẳng $\left(\alpha \right)$?

A. a // b và $b\subset \left(\alpha \right)$;

B. a // b và $b\cap \left(\alpha \right)=\varnothing$;

C. a // b và $b\text{//}\left(\alpha \right)$;

D. $a\cap \left(\alpha \right)=\varnothing$.

Câu 34. ABCD. Gọi M, N lần lượt là trung điểm của AB và AC. Đường thẳng MN song song với mặt phẳng

A. (ACD);

B. (ABD);

C. (BCD);

D. (ABC).

Câu 35. Cho tứ diện ABCD có G là trọng tâm của tam giác ABD, Q thuộc cạnh AB sao cho AQ = 2QB, P là trung điểm của AB. Khi đó

A. MN // (BCD);

B. GQ // (BCD);

C. MN cắt (BCD);

D. Q thuộc mặt phẳng (CDP).

PHẦN II. TỰ LUẬN (3,0 điểm)

Bài 1. (1,0 điểm) Giải các phương trình lượng giác:

a) $\cos \left(3x+\frac{\pi }{6}\right)-\sin \left(\frac{\pi }{3}-3x\right)=\sqrt{3}$;b) $\sin x+\sin 2x+\sin 3x=0$.

Bài 2. (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thang (hai đáy AB > CD). Gọi M, N lần lượt là trung điểm của SA, SB.

a) Tìm giao điểm P của SC và mp (ADN).

b) Biết AN cắt DP tại I. Chứng minh SI // AB. Tứ giác SABI là hình gì?

Bài 3. (1,0 điểm) Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình $x=3\cos \left(4\pi t-\frac{2\pi }{3}\right)$ , với t là thời gian tính bằng giây và x là quãng đường tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?

-----HẾT-----