Các hàm số lượng giác

Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với Sinx

1Làm xong biết đáp án, phương pháp giải chi tiết.
2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
4Biết điểm yếu và có hướng giải pháp cải thiện

Bắt đầu luyện tập

Số câu đúng

0/28

Thời gian làm bài

00:00:00

Số câu đã làm

Câu 1:

Hàm số y = sinx có tập xác định là:

A. R\{kπ, kϵZ}

B. R\ $\{\frac{k π}{2}, k \in Z\}$

C. R\ $\{\frac{π}{2} + k π, k \in Z\}$

D. R

Câu 2:

Tập giá trị của hàm số y=sinx là:

A. (−1;1)

B. [−1;1]

C. R

D. [0;1]

Câu 3:

Hàm số y=cosx nghịch biến trên mỗi khoảng:

A. $\{\frac{π}{2} + k 2 π, \frac{3 π}{2} + k 2 π\}$

B. (−π + k2π; k2π)

C. (k2π; π + k2π)

D. R

Câu 4:

Đồ thị hàm số y = tanx luôn đi qua điểm nào dưới đây?

A. O(0; 0)

B. M(0; 1)

C. $N (\frac{π}{2}; 0)$

D. P(1; 0)

Câu 5:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin2x+cos22x

y = 2sin² x + cos² 2x:

A. $\max y = 4; \min y = \frac{3}{4}$

B. max y = 3; min y = 2

C. max y = 4; min y = 2

D. $\max y = 3; \min y = \frac{3}{4}$

Câu 6:

Tìm tập xác định của hàm số $y = \tan (2 x - \frac{π}{4})$

A. D = R\ $\{\frac{π}{8} + \frac{k π}{2}, k \in Z\}$

B. D = R\ $\{\frac{3 π}{8} + \frac{k π}{2}, k \in Z\}$

C. D = R\ $\{\frac{3 π}{8} + k π, k \in Z\}$

D. D = R\

\{\frac{3 π}{4} + \frac{k π}{2}, k \in Z\}

Câu 7:

Hàm số $y = \frac{1 - \sin 2 x}{\cos 3 x - 1}$ xác định trên

A. D = R\ $\{\frac{k 2 π}{3}, k \in Z\}$

B. D = R\ $\{\frac{π}{6} + \frac{k π}{3}, k \in Z\}$

C. D = R\ $\{\frac{k π}{3}, k \in Z\}$

D. D = R\

\{\frac{k π}{2}, k \in Z\}

Câu 8:

Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau

y = 1 + 3 \sin (2 x - \frac{π}{4})

A. max y = - 2, min y = 4

B. max y = 2, min y = - 4

C. max y = - 2, min y = 3

D. max y = 4, min y = - 2

Câu 9:

Chọn mệnh đề đúng:

A. Hàm số y = sinx có chu kỳ T = π

B. Hàm số y = cosx và hàm số y = tanx có cùng chu kỳ.

C. Hàm số y = cotx và hàm số y = tanx có cùng chu kỳ.

D. Hàm số y = cotx có chu kỳ T = 2π

Câu 10:

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = \frac{4}{1 + 2 \sin^{2} x}$

A. $\min y = \frac{4}{3}; \max y = 4$

B. $\min y = \frac{4}{3}; \max y = 3$

C. $\min y = \frac{4}{3}; \max y = 2$

D. $\min y = \frac{1}{2}; \max y = 2$

Câu 11:

Tìm tập xác định của hàm số

y = \sqrt{\frac{1 - \cos 3 x}{1 + \sin 4 x}}

A. D = R\ $\{- \frac{π}{8} + k \frac{π}{4}, k \in Z\}$

B. D = R\ $\{- \frac{3 π}{8} + k \frac{π}{2}, k \in Z\}$

C. D = R\ $\{- \frac{π}{8} + k \frac{π}{2}, k \in Z\}$

D. D = R\

\{\frac{k 2 π}{3}, k \in Z\}

Câu 12:

Hình nào dưới đây biểu diễn đồ thị hàm số y = f(x) = 2 sin 2x

A. 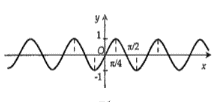Media VietJack

B. 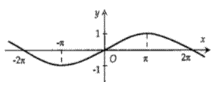Media VietJac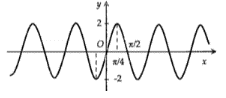k

C. Med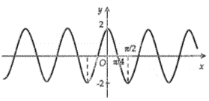ia VietJack

D. Media VietJack

Câu 13:

Xét sự biến thiên của hàm số y = 1 − sinx trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?

A. Hàm số đã cho nghịch biến trên khoảng $(- \frac{π}{2}; 0)$

B. Hàm số đã cho nghịch biến trên khoảng $(0; \frac{π}{2})$

C. Hàm số đã cho đồng biến trên khoảng $(\frac{π}{2}; π)$

D. Hàm số đã cho nghịch biến trên khoảng

(\frac{π}{2}; \frac{3 π}{2})

Câu 14:

Hàm số nào trong các hàm số sau có đồ thị nhận OyOy làm trục đối xứng ?

A, $y = |x| \sin x$

B. $y = \sin x . \cos^{2} x + \tan x$

C. $y = \frac{\sin^{2020} x + 2019}{\cos x}$

D.y = tan x

Câu 15:

Cho các mệnh đề sau :

(I): Hàm số y = sinx có chu kì là $\frac{π}{2}$ .

(II): Hàm số y = tanx có tập giá trị là R∖ $\{\frac{π}{2} + k π |k \in Z\}$

(III): Đồ thị hàm số y = cosx đối xứng qua trục tung.

(IV): Hàm số y = cotx nghịch biến trên (−π; 0)

Có bao nhiêu mệnh đề đúng trong các mệnh đề trên ?

A. 2

B. 4

C. 1

D. 3

Câu 16:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y = \sqrt{2 \sin x + 3}$

A. $\max y = \sqrt{5}, miny = 1$

B. $\max y = \sqrt{5}, miny = 0$

C. $\max y = \sqrt{5}, miny = \sqrt{3}$

D. $\max y = \sqrt{5}, miny = 3$

Câu 17:

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = 3sinx + 4cosx − 1

A. min y = −6; max y = 4

B. min y = −5; max y = 5

C. min y = −3; max y = 4

D. min y = −6; max y = 6

Câu 18:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

y = cos2x + cosx. Khi đó M + m bằng bao nhiêu?

A. $M + n = \frac{9}{8}$

B. $M + n = \frac{9}{7}$

C. $M + n = \frac{8}{7}$

D. $M + n = \frac{7}{8}$

Câu 19:

Có bao nhiêu giá trị xϵ[0; 5π] để hàm số y = tanx nhận giá trị bằng 0?

A. 9

B. 10

C. 7

D. 6

Câu 20:

Khẳng định nào sau đây là đúng?

A. y = |tanx| đồng biến trong $[- \frac{π}{2}; \frac{π}{2}]$

B. y = |tanx| là hàm số chẵn trên D = R\ $\{\frac{π}{2} + k π |k \in Z\}$

C. y = |tanx| có đồ thị đối xứng qua gốc tọa độ.

D. y = |tanx| luôn nghịch biến trong

(- \frac{π}{2}; \frac{π}{2})

Câu 21:

Xét sự biến thiên của hàm số y = sinx − cosx. Trong các kết luận sau, kết luận nào đúng?

A. Hàm số đã cho đồng biến trên khoảng $(- \frac{π}{4}; \frac{3 π}{4})$

B. Hàm số đã cho đồng biến trên khoảng $(\frac{3 π}{4}; \frac{7 π}{4})$

C. Hàm số đã cho có tập giá trị là [−1;1].

D. Hàm số đã cho luôn nghịch biến trên khoảng

(- \frac{π}{4}; \frac{7 π}{4})

Câu 22:

Giá trị nhỏ nhất của hàm số y = 2 cos²x + sin2x là:

A. $2 \sqrt{2}$

B. $1 - \sqrt{2}$

C. $1 + \sqrt{2}$

D. 3

Câu 23:

Tìm m để hàm số $y = \sqrt{8 \cos x - 6 \sin x - {(3 \sin x - 4 \cos x)}^{2} - 2 m}$ có tập xác định là R.

A. $m \leq - \frac{35}{2}$

B. $m \leq - 35$

C. $m \leq \frac{1}{2}$

D. $m \leq \frac{- 3}{2}$

Câu 24:

Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau $y = \frac{\sin 2 x + 2 \cos 2 x + 3}{2 \sin 2 x - \cos 2 x + 4}$

A. $\min y = - \frac{2}{11}; \max y = 2$

B. $\min y = \frac{2}{11}; \max y = 3$

C. $\min y = \frac{2}{11}; \max y = 4$

D. $\min y = \frac{2}{11}; \max y = 2$

Câu 25:

Tìm tập giá trị lớn nhất, nhỏ nhất của hàm số sau: $y = 3 {(3 \sin x + 4 \cos x)}^{2} + 4 (3 \sin x + 4 \cos x) + 1$

A. $\min y = \frac{1}{3}; \max y = 96$

B. $\min y = \frac{1}{3}; \max y = 6$

C. $\min y = - \frac{1}{3}; \max y = 96$

D. $\min y = 2; \max y = 6$

Câu 26:

Tìm m để bất phương trình

\frac{3 \sin 2 x + \cos 2 x}{\sin 2 x + 4 \cos^{2} x + 1} \leq m + 1

đúng với mọi x∈R

A. $m \geq \frac{\sqrt{65}}{4}$

B. $m \geq \frac{\sqrt{65} + 9}{4}$

C. $m \geq \frac{\sqrt{65} - 9}{2}$

D. $m \geq \frac{\sqrt{65} - 9}{4}$

Câu 27:

Cho hàm số lượng giác

f (x) = \tan x - \frac{1}{\sin x}

Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số trên.

A. Hàm tuần hoàn với chu kì T = 2π.

B. Hàm tuần hoàn với chu kì T = π.

C. Hàm tuần hoàn với chu kì T = 3π.

D. Hàm số không tuần hoàn.

Câu 28:

Cho hàm số lượng giác $f (x) = \tan x - \frac{1}{\sin x}$

Xét tính chẵn, lẻ của hàm số trên.

A. Hàm số f(x) là hàm số chẵn

B. Hàm số f(x) là hàm số vừa chẵn vừa lẻ.

C. Hàm số f(x) là hàm số lẻ.

D. Hàm số f(x) là hàm số không có tính chẵn lẻ.

Các hàm số lượng giác

Giới thiệu

Liên kết

Chính sách

Kết nối

Các hàm số lượng giác

CHỌN BỘ SÁCH BẠN MUỐN XEM