Cách viết giả thiết, kết luận, vẽ hình và chứng minh một định lí
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Giả thiết và kết luận của định lí trên là:
A.
|
GT |
x ⊥ y; y // z |
|
KL |
x ⊥ z |
B.
|
GT |
x // y; y // z |
|
KL |
x ⊥ z |
C.
|
GT |
x ⊥ y; y ⊥ z |
|
KL |
x // z |
D.
|
GT |
x ⊥ y; y // z |
|
KL |
x // z |
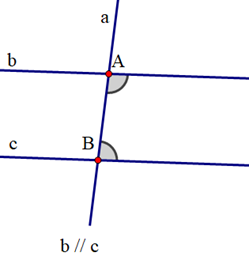
Phát biểu định lí sau bằng lời:
|
GT |
a // b; c // b; a ≠ c |
|
KL |
a // c |
Phát biểu định lí sau bằng lời:
|
GT |
a ⊥ b; c ⊥ b; a ≠ c |
|
KL |
a // c |
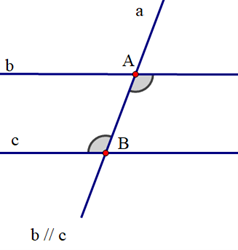
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc trong cùng phía bù nhau” và hình vẽ minh hoạ sau:
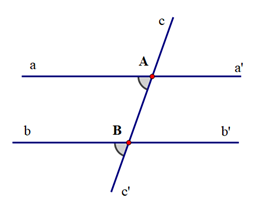
Hãy viết giả thiết, kết luận cho định lý trên:
A.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'}\] |
|
KL |
\[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
B.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb' |
|
KL |
\[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
C.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] |
|
KL |
\[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
D.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] |
|
KL |
\[\widehat {{\rm{aA}}B} = \widehat {ABb};\] \[\widehat {{\rm{a'A}}B} = \widehat {ABb'};\] |
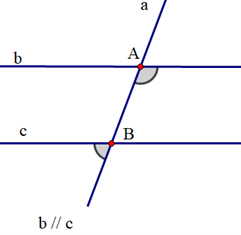
Cho hình vẽ:
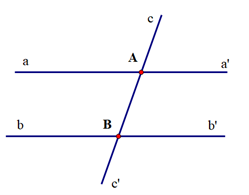
Bảng sau là giả thiết, kết luận của định lí nào?
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B (aa' ≠ bb') \[\widehat {aAB}\] + \[\widehat {ABb}\] = 180° |
|
KL |
\[\widehat {aAB} = \widehat {ABb'};\]\[\widehat {a'AB} = \widehat {ABb}\] |
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
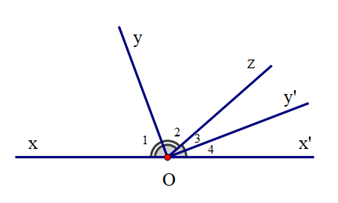
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra Oy vuông góc với Oy'
Vậy định lí được chứng minh.”;
(II). “Vì Oy' là tia phân giác của \(\widehat {x'Oz}\) (giả thiết) nên \({\widehat O_3} = \frac{1}{2}\widehat {x'Oz}\)”;
(III) “Mà \(\widehat {xOz}\) và \(\widehat {zOx'}\)là hai góc kề bù (giả thiết)
Nên \(\widehat {xOz} + \widehat {zOx'} = 180^\circ \) (tính chất hai góc kề bù)
Do đó \(\widehat {yOy'} = \frac{1}{2}{.180^o} = {90^o}\)”;
(IV). “Có \(\widehat {yOy'} = {\widehat O_2} + {\widehat O_3}\)\( = \frac{1}{2}\widehat {xOz} + \frac{1}{2}\widehat {x'Oz}\)\( = \frac{1}{2}\left( {\widehat {xOz} + \widehat {zOx'}} \right)\)”
(V). “Vì Oy là tia phân giác của \(\widehat {xOz}\)(giả thiết) nên \({\widehat O_2} = \frac{1}{2}\widehat {xOz}\)”.
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” và hình vẽ minh hoạ sau:
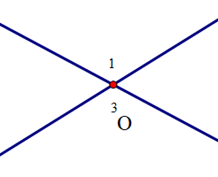
Viết giả thiết, kết luận cho định lí trên:
A.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} + {\widehat O_3} = 180^\circ \) |
B.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
C.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
D.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_3} = {\widehat O_4}\) |
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” được minh hoạ bởi hình vẽ sau:
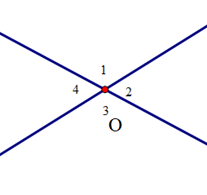
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra \({\widehat O_1} = {\widehat O_3}\) (vì cùng bù với \({\widehat O_2}\))”;
(II). “Ta có: \({\widehat O_1} + {\widehat O_2} = 180^\circ \)(hai góc kề bù) và \({\widehat O_2} + {\widehat O_3} = 180^\circ \)(hai góc kề bù)”;
(III). “Suy ra \({\widehat O_2} = {\widehat O_4}\) (vì cùng bù với \({\widehat O_3}\))
Vậy định lí được chứng minh.”;
(IV). “Lại có: \[{\widehat O_2} + {\widehat O_3} = 180^\circ \](hai góc kề bù) và \({\widehat O_3} + {\widehat O_4} = 180^\circ \)(hai góc kề bù)”.
Các bài liên quan
Kiến thức bổ ích có thể giúp đỡ bạn rất nhiều:
