Lý thuyết Cách viết giả thiết, kết luận, vẽ hình và chứng minh một định lí
- Cách viết giả thiết, kết luận:
Ta có thể viết giả thiết và kết luận của định lí bằng kí hiệu như sau:
|
GT |
Những điều cho biết trước |
|
KL |
Những điều cần suy ra |
- Cách vẽ hình:
Sử dụng các dữ kiện giả thiết cho để vẽ hình trong trường hợp cụ thể.
- Cách chứng minh một định lí:
Dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.
Ví dụ 1. Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau”.
a) Viết giả thiết, kết luận của định lí trên;
b) Vẽ hình;
c) Chứng minh định lí.
Hướng dẫn giải:
a)
|
GT |
aa' cắt cc’ tại A; bb' cắt cc’ tại B; \[\widehat {aAB} = \widehat {ABb'}\] |
|
KL |
\[\widehat {cAa'} = \widehat {ABb'}\] \[\widehat {aAB} = \widehat {bBc'}\] \[\widehat {aAc} = \widehat {bBA}\] \[\widehat {a'AB} = \widehat {b'Bc'}\] |
b)
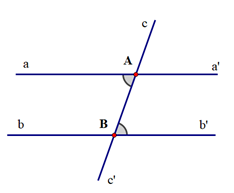
c) + Ta có \[\widehat {aAB} = \widehat {ABb'}\] (giả thiết)
Mà \[\widehat {aAB} = \widehat {cAa'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {cAa'} = \widehat {ABb'}\] (vì cùng bằng \[\widehat {aAB}\]).
+ Ta có \[\widehat {aAB} = \widehat {ABb'}\](giả thiết)
Mà \[\widehat {ABb'} = \widehat {bBc'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {aAB} = \widehat {bBc'}\] (vì cùng bằng \[\widehat {ABb'}\]).
+ Ta có \[\widehat {aAc}\] + \[\widehat {BAa}\] = 180° (hai góc kề bù)
Và \[\widehat {bBA}\] + \[\widehat {ABb'}\] = 180° (hai góc kề bù)
Mà \[\widehat {aAB} = \widehat {ABb'}\]
Suy ra \[\widehat {aAc}\] = \[\widehat {bBA}\].
+ Ta có \[\widehat {a'AB}\] = \[\widehat {aAc}\] (hai góc đối đỉnh)
\[\widehat {b'Bc'}\] = \[\widehat {bBA}\] (hai góc đối đỉnh)
Mà \[\widehat {aAc}\] = \[\widehat {bBA}\]
Suy ra \[\widehat {a'AB} = \widehat {b'Bc'}\].
Vậy định lí được chứng minh.
Ví dụ 2. Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau”.
a) Viết giả thiết, kết luận của định lí trên;
b) Vẽ hình cho định lí trên;
c) Chứng minh định lí.
Hướng dẫn giải:
a)
|
GT |
aa' cắt cc’ tại A; bb' cắt cc’ tại B; aa’ // bb’ |
|
KL |
\[\widehat {aAB} + \widehat {ABb} = 180^\circ ;\] \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ \] |
b)
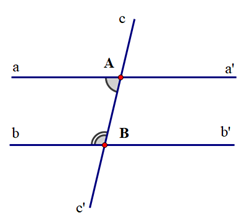
c)
+ Ta có aa’ // bb’ (giả thiết) nên \[\widehat {aAB} = \widehat {ABb'}\] (hai góc so le trong)
Vì \[\widehat {ABb}\] và \[\widehat {ABb'}\] là hai góc kề bù nên \[\widehat {ABb} + \widehat {ABb'} = 180^\circ \]
Suy ra \[\widehat {ABb} + \widehat {aAB} = 180^\circ \]
+ Ta có aa’ // bb’ (giả thiết) nên \[\widehat {a'AB} = \widehat {ABb}\] (hai góc so le trong)
Mà \[\widehat {ABb} + \widehat {ABb'} = 180^\circ \] (chứng minh trên)
Suy ra \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ \]
Vậy định lí được chứng minh.