Lý thuyết Tìm và chứng minh hai tam giác vuông bằng nhau

Bước 1: Xét hai tam giác vuông.

Bước 2: Kiểm tra tất cả các điều kiện của một trong các trường hợp bằng nhau của hai tam giác vuông: hai cạnh góc vuông; cạnh huyền – góc nhọn; cạnh huyền – cạnh góc vuông; cạnh góc vuông – góc nhọn kề.

Bước 3: Kết luận hai tam giác vuông bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

Ví dụ 1. Tìm các cặp tam giác vuông bằng nhau và giải thích tại sao chúng bằng nhau trong hình dưới đây.

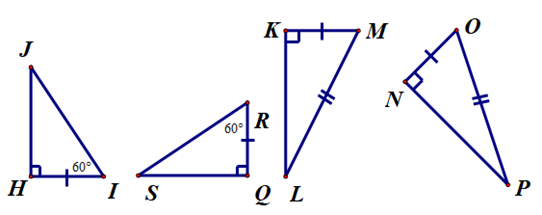
Hướng dẫn giải:

Xét ∆HIJ (vuông tại H) và ∆QRS (vuông tại Q), có:

HI = QR (giả thiết),

\[\widehat {HIJ} = \widehat {QRS}\left( { = 60^\circ } \right)\].

Do đó ∆HIJ = ∆QRS (cạnh góc vuông – góc nhọn kề).

Xét ∆KML (vuông tại K) và ∆NOP (vuông tại N), có:

MK = ON (giả thiết),

ML = OP (giả thiết).

Do đó ∆KML = ∆NOP (cạnh huyền – cạnh góc vuông).

Vậy ta có hai cặp tam giác bằng nhau là:

+ ∆HIJ = ∆QRS (cạnh góc vuông – góc nhọn kề);

+ ∆KML = ∆NOP (cạnh huyền – cạnh góc vuông).

Ví dụ 2. Cho ∆ABC có AB = AC, AM là tia phân giác của \[\widehat A\] (M ∈ BC). Kẻ MD vuông góc AB tại D, ME vuông góc AC tại E. Chứng minh rằng ∆AMD = ∆AME.

Hướng dẫn giải:

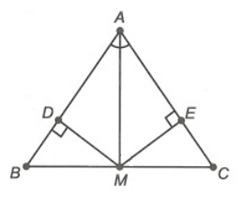
Xét ∆AMD và ∆AME, có:

\[\widehat {ADM} = \widehat {AEM} = 90^\circ \] (MD ⊥ AB tại D, ME ⊥ AC tại E).

AM là cạnh chung.

\[\widehat {DAM} = \widehat {EAM}\] (AM là tia phân giác của \[\widehat A\]).

Do đó ∆AMD = ∆AME (cạnh huyền – góc nhọn).

Vậy ∆AMD = ∆AME.