Lý thuyết Nhận biết và chứng minh tam giác cân, tam giác đều
a) Nhận biết và chứng minh tam giác cân
Để nhận biết và chứng minh một tam giác là tam giác cân, ta sử dụng một trong hai cách sau:
Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau. Khi đó tam giác đó cân tại giao điểm của hai cạnh đó;
Cách 2: Chứng minh tam giác đó có hai góc bằng nhau. Khi đó tam giác đó cân tại đỉnh còn lại.
Lưu ý: Khi chứng minh một tam giác là tam giác cân, ta cần chỉ rõ tam giác đó cân tại đỉnh nào. Ví dụ ∆ABC cân tại A, ∆MNP cân tại N,...
b) Nhận biết và chứng minh tam giác đều
Để nhận biết và chứng minh một tam giác là tam giác đều, ta sử dụng một trong bốn cách sau:
Cách 1: Chứng tỏ tam giác đó có ba cạnh bằng nhau;
Cách 2: Chứng tỏ tam giác đó có ba góc bằng nhau;
Cách 3: Chứng tỏ tam giác đó có hai góc bằng 60°;
Cách 4: Chứng tỏ tam giác đó là tam giác cân và có một góc bằng 60°.
Ví dụ 1. Cho hình vẽ bên.
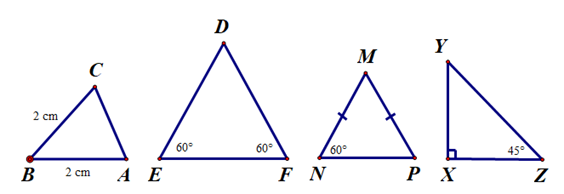
Hỏi tam giác nào là tam giác cân, tam giác nào là tam giác đều?
Hướng dẫn giải:
+ Xét ∆ABC, có: AB = BC = 2 cm.
Do đó ∆ABC cân tại B.
+ Xét ∆DEF, có: \[\widehat {DEF} = \widehat {DFE} = 60^\circ \].
Do đó ∆DEF là tam giác đều.
+ Xét ∆MNP, có: MN = MP và \[\widehat {MNP} = 60^\circ \].
Do đó ∆MNP là tam giác đều.
+ ∆XYZ vuông tại X: \[\widehat Y + \widehat Z = 90^\circ \].
Suy ra \[\widehat Y = 90^\circ - \widehat Z = 90^\circ - 45^\circ = 45^\circ \].
Do đó \[\widehat Y = \widehat Z = 45^\circ \].
Suy ra ∆XYZ cân tại X.
(Vì ∆XYZ cân tại X và có \[\widehat X = 90^\circ \], do đó ta gọi ∆XYZ là tam giác vuông cân tại X).
Vậy ở hình bên, ta có:
- Các tam giác cân là: ∆ABC (cân tại B) và ∆XYZ (vuông cân tại X).
- Các tam giác đều là: ∆DEF và ∆MNP.
Ví dụ 2. Cho ba điểm A, B, C thẳng hàng theo thứ tự đó. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều ACD, BCE. Gọi I, K theo thứ tự là trung điểm của AE và BD. Chứng minh rằng ∆CIK là tam giác đều.
Hướng dẫn giải:
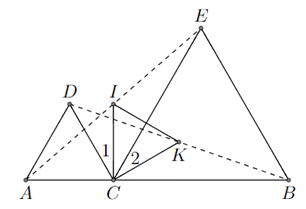
Ta có ∆ACD đều. Suy ra \[\widehat {ACD} = 60^\circ \] (1).
Ta có ∆BCE đều. Suy ra \[\widehat {ECB} = 60^\circ \] (2).
Từ (1), (2), ta suy ra \[\widehat {ACD} = \widehat {ECB}\].
Do đó \[\widehat {ACD} + \widehat {DCE} = \widehat {ECB} + \widehat {DCE}\].
Khi đó ta có \[\widehat {ACE} = \widehat {DCB}\].
Xét ∆ACE và ∆DCB, có:
AC = DC (∆ACD đều).
\[\widehat {ACE} = \widehat {DCB}\] (chứng minh trên).
CE = CB (∆BCE đều).
Do đó ∆ACE = ∆DCB (cạnh – góc – cạnh).
Suy ra \[\widehat {CAE} = \widehat {CDB}\] và AE = DB (cặp góc và cặp cạnh tương ứng).
Vì I là trung điểm AE nên ta có AE = 2AI.
Vì K là trung điểm DB nên ta có DB = 2DK.
Mà AE = DB (chứng minh trên).
Do đó 2AI = 2DK.
Suy ra AI = DK.
Xét ∆ACI và ∆DCK, có:
AC = DC (∆ACD đều).
\[\widehat {CAE} = \widehat {CDB}\] (chứng minh trên).
AI = DK (chứng minh trên).
Do đó ∆ACI = ∆DCK (cạnh – góc – cạnh).
Suy ra CI = CK.
Do đó ∆CIK cân tại C (*).
Ta có \[\widehat {ACI} = \widehat {DCK}\] (vì ∆ACI = ∆DCK).
Do đó \[\widehat {ACD} + \widehat {DCI} = \widehat {DCI} + \widehat {ICK}\].
Ta suy ra \[\widehat {ACD} = \widehat {ICK}\].
Mà \[\widehat {ACD} = 60^\circ \] (∆ACD đều).
Do đó \[\widehat {ICK} = \widehat {ACD} = 60^\circ \] (**).
Từ (*), (**), ta suy ra ∆CIK là tam giác đều.