Lý thuyết Áp dụng các công thức tính diện tích xung quanh và thể tích để giải các bài toán thực tế

Để giải các bài toán thực tế liên quan đến diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương ta áp dụng các công thức tính diện tích xung quanh, thể tích của hình lập phương và hình hộp chữ nhật.

- Cho hình hộp chữ nhật có có chiều dài là a, chiều rộng là b và chiều cao là h (như hình vẽ).

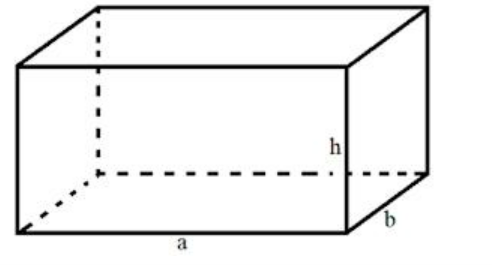
Diện tích xung quanh của hình hộp chữ nhật là:

S_xq = 2 . (a + b) . h

Tổng diện tích các mặt (hay diện tích toàn phần) của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích hai mặt đáy của hình hộp chữ nhật và bằng:

S_tp = S_xq + 2ab = 2 . (a + b) . h + 2ab = 2 . (ab + ah + bh)

Thể tích của hình hộp chữ nhật là:

V = a . b . h = S . h (trong đó S là diện tích đáy).

- Cho hình lập phương có độ dài độ dài một cạnh bằng a (như hình vẽ).

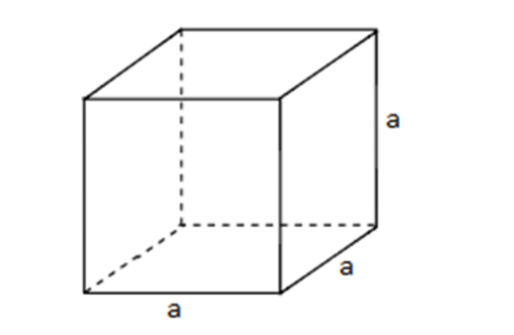
Diện tích xung quanh của hình lập phương là: S_xq = 4 . a².

Tổng diện tích các mặt (hay diện tích toàn phần) của hình lập phương là tổng diện tích sáu mặt của hình lập phương là:

S_tp = 6 . a².

Thể tích của hình lập phương là: V = a³.

Ví dụ 1. Một người làm cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh 14 cm. Tính diện tích bìa cần dùng để làm hộp (không tính mép dán).

Hướng dẫn giải:

Diện tích một mặt của cái hộp đó là:

14 . 14 = 196 (cm²)

Diện tích bìa cần dùng để làm cái hộp đó là:

196 . 5 = 980 (cm²)

Vậy diện tích bìa cần dùng để làm cái hộp đó là 980 cm².

Ví dụ 2. Một chiếc bánh kem dạng hình hộp chữ nhật với chiều dài 30 cm, chiểu rộng 20 cm và chiều cao 15 cm. Người ta cắt đi một miếng bánh có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của chiếc bánh kem.

Hướng dẫn giải:

Thể tích chiếc bánh kem dạng hình hộp chữ nhật là:

30 . 20 . 15 = 9 000 (cm³)

Thể tích phần bánh cắt đi là:

5³ =125 (cm³)

Thể tích phần còn lại của chiếc bánh kem là:

9 000 – 125 = 8 875 (cm³)

Vậy thể tích phần còn lại của chiếc bánh kem là 8 875 cm³.