Lý thuyết Tính số đo góc trong tam giác dựa vào định lí tổng ba góc trong một tam giác và góc ngoài của một tam giác

Để tính số đo của một góc trong tam giác, ta thực hiện các bước sau:

Bước 1: Lập các đẳng thức thể hiện:

+ Tổng ba góc của một tam giác bằng 180°;

+ Trong tam giác vuông, hai góc nhọn phụ nhau;

+ Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó;

+ Ngoài ra ta có thể vận dụng: tính chất hai góc kề bù, hai góc đối đỉnh, tính chất tia phân giác của một góc, tính chất hai đường thẳng song song,…

Bước 2: Từ các đẳng thức đã lập được ta tính số đo góc cần tìm.

Ví dụ 1. Tính số đo góc x, y, z trong các hình dưới đây:

Hướng dẫn giải

Hình 1:

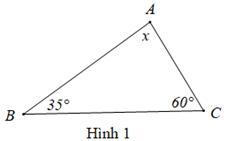
Xét tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(x = \widehat A = 180^\circ  - \widehat B - \widehat C\)

Mà \(\widehat B = 35^\circ ,\widehat C = 60^\circ \)

Do đó x = 180° ‒ 35° ‒ 60° = 85°

Vậy x = 85°.

Hình 2:

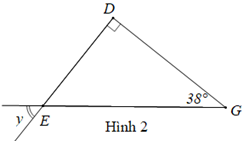
Tam giác DEG có \(\widehat D = 90^\circ \) nên tam giác DEG là tam giác vuông tại D.

Suy ra \(\widehat {DEG} + \widehat G = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)

Hay \(\widehat {DEG} = 90^\circ  - \widehat G = 90^\circ  - 38^\circ  = 52^\circ \)

Mà \(y = \widehat {DEG}\) (hai góc đối đỉnh)

Do đó y = 52°.

Vậy y = 52°.

Hình 3:

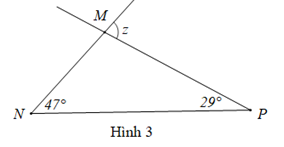
Tam giác MNP có góc z là góc ngoài của tam giác tại đỉnh M

Nên \(z = \widehat N + \widehat P\) (tính chất góc ngoài của tam giác)

Do đó z = 47° + 29° = 76°

Vậy z = 76°.

Ví dụ 2. Tìm số đo góc CAE trong hình dưới đây:

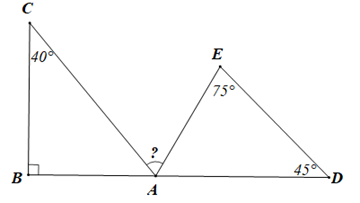
Hướng dẫn giải

Xét tam giác ABC có \(\widehat B = 90^\circ \) nên tam giác ABC vuông tại B.

Do đó \(\widehat {BAC} + \widehat C = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra \(\widehat {BAC} = 90^\circ  - \widehat C\)

Hay \(\widehat {BAC} = 90^\circ  - 40^\circ  = 50^\circ \)

Xét tam giác ADE có \(\widehat {BAE}\) là góc ngoài của tam giác tại đỉnh A

Nên \(\widehat {BAE} = \widehat D + \widehat E\) (tính chất góc ngoài của tam giác)

Hay \(\widehat {BAE} = 45^\circ  + 75^\circ  = 120^\circ \)

Ta lại có: \(\widehat {BAC}\) và \(\widehat {CAE}\) là hai góc kề nhau nên \[\widehat {BAC} + \widehat {CAE} = \widehat {BAE}\]

Suy ra \(\widehat {CAE} = \widehat {BAE} - \widehat {BAC}\)

Hay \(\widehat {CAE} = 120^\circ  - 50^\circ  = 70^\circ \)

Vậy số đo góc CAE bằng 70°.