Lý thuyết Sử dụng trường hợp bằng nhau của hai tam giác vuông để chứng minh tính chất khác
Bước 1: Chọn hai tam giác vuông có cạnh (góc) là hai đoạn thẳng (góc) cần chứng minh bằng nhau.
Bước 2: Chứng minh hai tam giác vuông bằng nhau theo một trong các trường hợp bằng nhau của hai tam giác vuông: hai cạnh góc vuông; cạnh góc vuông – góc nhọn kề; cạnh huyền – góc nhọn, cạnh huyền – cạnh góc vuông.
Bước 3: Suy ra hai cạnh (góc) tương ứng bằng nhau và kết luận.
Ví dụ 1. Cho ∆ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD ⊥ xy tại D, kẻ CE ⊥ xy tại E. Chứng minh rằng:
a) ∆BAD = ∆ACE;
b) DE = BD + CE.
Hướng dẫn giải:
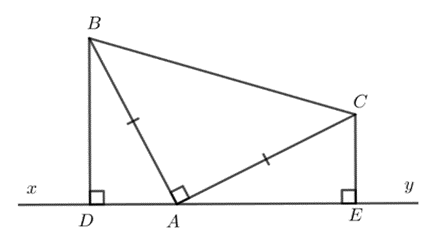
Tam giác ABD vuông tại D: \[\widehat {DAB} + \widehat {ABD} = 90^\circ \] (1).
Tam giác ABC vuông tại A. Ta suy ra \[\widehat {BAC} = 90^\circ \].
Ta có: \[\widehat {DAB} + \widehat {BAC} + \widehat {CAE} = 180^\circ \].
\[ \Leftrightarrow \widehat {DAB} + 90^\circ + \widehat {CAE} = 180^\circ \].
\[ \Leftrightarrow \widehat {DAB} + \widehat {CAE} = 180^\circ - 90^\circ = 90^\circ \] (2).
Từ (1), (2), ta suy ra \[\widehat {ABD} = \widehat {CAE}\].
Xét ∆BAD và ∆ACE, có:
\[\widehat {ADB} = \widehat {AEC} = 90^\circ \].
AB = AC (giả thiết).
\[\widehat {ABD} = \widehat {CAE}\] (chứng minh trên).
Do đó ∆BAD = ∆ACE (cạnh huyền – góc nhọn).
b) Ta có: ∆BAD = ∆ACE (chứng minh trên)
Ta suy ra AD = CE và BD = AE (các cặp cạnh tương ứng bằng nhau).
Do đó AD + AE = CE + BD.
Suy ra DE = CE + BD (vì A nằm giữa D và E).
Vậy DE = BD + CE.
Ví dụ 2. Cho tam giác ABC vuông tại A. Kẻ AH ⊥ BC tại H. Trên tia đối của tia HA, lấy điểm D sao cho HD = HA.
a) Chứng minh rằng ∆AHB = ∆DHB;
b) Chứng minh rằng BD ⊥ CD.
c) Cho \[\widehat {ABC} = 60^\circ \]. Tính số đo \[\widehat {ACD}\].
Hướng dẫn giải:
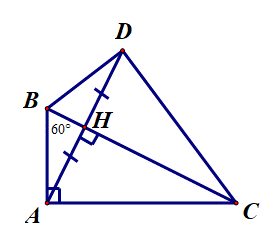
a) Xét ∆AHB và ∆DHB, có:
\[\widehat {AHB} = \widehat {DHB} = 90^\circ \].
HB là cạnh chung.
HA = HD (giả thiết).
Do đó ∆AHB = ∆DHB (hai cạnh góc vuông).
b) Ta có ∆AHB = ∆DHB (chứng minh trên).
Do đó AB = DB và \[\widehat {ABH} = \widehat {DBH}\] (các cặp cạnh, cặp góc tương ứng bằng nhau).
Xét ∆ABC và ∆DBC, có:
AB = DB (chứng minh trên).
BC là cạnh chung.
\[\widehat {ABC} = \widehat {DBC}\] (chứng minh trên).
Do đó ∆ABC = ∆DBC (cạnh – góc – cạnh).
Ta suy ra \[\widehat {BDC} = \widehat {BAC} = 90^\circ \] (hai góc tương ứng)
Vậy BD ⊥ CD.
c) ∆ABC vuông tại A: \[\widehat {ABC} + \widehat {ACB} = 90^\circ \] (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \[\widehat {ACB} = 90^\circ - \widehat {ABC} = 90^\circ - 60^\circ = 30^\circ \].
Ta có ∆ABC = ∆DBC (chứng minh trên).
Ta suy ra \[\widehat {ACB} = \widehat {BCD}\] (cặp góc tương ứng bằng nhau).
Do đó \[\widehat {BCD} = \widehat {ACB} = 30^\circ \].
Ta có \[\widehat {ACD} = \widehat {ACB} + \widehat {BCD} = 30^\circ + 30^\circ = 60^\circ \].
Vậy \[\widehat {ACD} = 60^\circ \].