Lý thuyết Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng

Để chứng minh đường thẳng d là đường trung trực của đoạn thẳng AB, ta sử dụng một trong hai cách sau:

Cách 1 (dùng định nghĩa): Chứng minh đường thẳng d vuông góc với đoạn thẳng AB tại trung điểm M của đoạn thẳng AB;

Cách 2 (dùng tính chất): Chứng minh đường thẳng d chứa hai điểm E, F cách đều A và B.

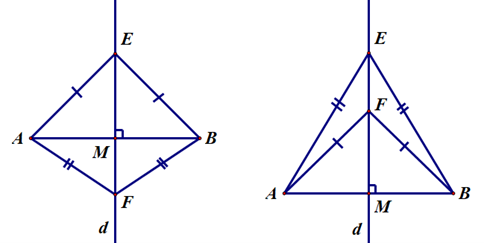
Ví dụ 1. Cho hình vẽ bên.

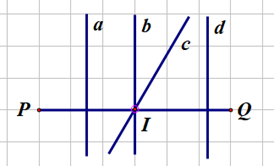
Đường thẳng nào là đường trung trực của đoạn thẳng PQ?

Hướng dẫn giải:

Một đường thẳng là đường trung trực của một đoạn thẳng khi thỏa mãn cả hai yếu tố sau:

+ Đi qua trung điểm của đoạn thẳng.

+ Vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.

- Ta thấy đường thẳng a và d không đi qua trung điểm I của đoạn thẳng PQ.

Do đó đường thẳng a và d không phải là đường trung trực của đoạn thẳng PQ.

- Đường thẳng b đi qua trung điểm I và vuông góc với đoạn thẳng PQ tại trung điểm I.

Do đó đường thẳng b là đường trung trực của đoạn thẳng PQ.

- Đường thẳng c đi qua trung điểm I nhưng không vuông góc với đoạn thẳng PQ tại trung điểm I.

Do đó đường thẳng c không phải là đường trung trực của đoạn thẳng PQ.

Vậy đường thẳng b là đường trung trực của đoạn thẳng PQ.

Ví dụ 2. Cho ∆ABC có AC = BC. Gọi I là trung điểm AB. Trên tia CI lấy điểm D sao cho D nằm khác phía với C (bờ là đường thẳng AB). Chứng minh CD là đường trung trực của AB.

Hướng dẫn giải:

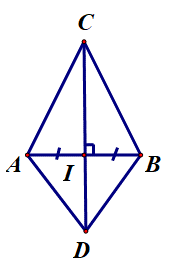
Cách 1:

Xét ∆CAI và ∆CBI, có:

CA = CB (giả thiết).

CI là cạnh chung.

AI = BI (I là trung điểm AB).

Do đó ∆CAI = ∆CBI (cạnh – cạnh – cạnh).

Suy ra \[\widehat {CIA} = \widehat {CIB}\] (cặp góc tương ứng).

Mà \[\widehat {CIA} + \widehat {CIB} = 180^\circ \] (hai góc kề bù).

Do đó \[\widehat {CIA} = \widehat {CIB} = 90^\circ \].

Khi đó ta có CI ⊥ AB.

Mà I là trung điểm của AB (giả thiết).

Suy ra CI là đường trung trực của AB.

Vậy CD là đường trung trực của AB.

Cách 2:

Xét ∆ADC và ∆BDC, có:

AC = BC (giả thiết).

CD là cạnh chung.

\[\widehat {ACD} = \widehat {BCD}\] (∆CAI = ∆CBI).

Do đó ∆ADC = ∆BDC (cạnh – góc – cạnh).

Suy ra AD = BD (cặp cạnh tương ứng).

Mà CA = CB (giả thiết).

Vậy CD là đường trung trực của AB.