Lý thuyết Nhận biết hai góc kề nhau, bù nhau, kề bù và đối đỉnh

a) Nhận biết hai góc kề nhau

* Để nhận biết hai góc kề nhau ta dựa vào hai dấu hiệu sau:

- Hai góc có một cạnh chung.

- Hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.

* Hình vẽ minh hoạ hai góc kề nhau:

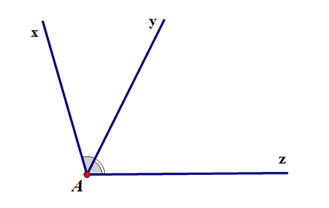
b) Nhận biết hai góc bù nhau

* Để nhận biết hai góc bù nhau ta dựa vào dấu hiệu: Hai góc có tổng số đo bằng 180^o.

* Hình vẽ minh hoạ hai góc bù nhau:

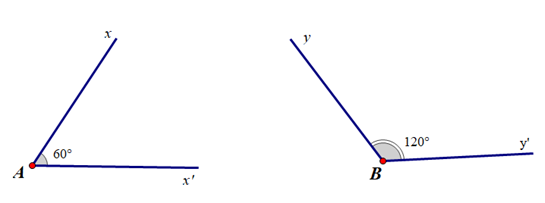
c) Nhận biết hai góc kề bù

* Có hai cách nhận biết hai góc kề bù:

- Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.

- Hai góc có một cạnh chung và hai cạnh còn lại là tia đối của nhau.

* Hình vẽ minh hoạ hai góc kề bù:

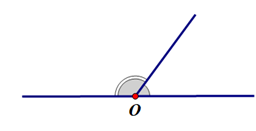
d) Nhận biết hai góc đối đỉnh

* Để nhận biết hai góc đối đỉnh ta dựa vào hai dấu hiệu sau:

- Hai góc có chung đỉnh.

- Các cạnh của góc này thuộc tia đối của cạnh góc kia.

* Hình vẽ minh hoạ hai góc đối đỉnh:

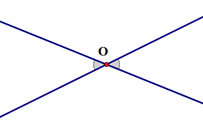
- Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh và hai góc đối đỉnh có số đo bằng nhau.

Ví dụ 1. Quan sát hình vẽ sau và cho biết:

a)  Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có kề với nhau không? Vì sao?

b) Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có bù với nhau không? Vì sao?

c) Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có kề bù với nhau không? Vì sao?

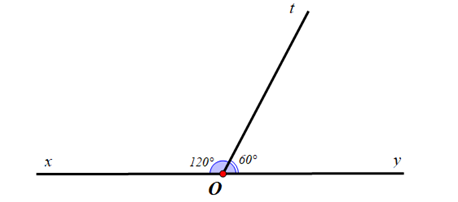
Hướng dẫn giải:

a) Ta có: \(\widehat {xOt},\widehat {tOy}\)là hai góc có một cạnh chung Ot và hai cạnh Ox, Oy nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung Ot.

Suy ra \(\widehat {xOt},\widehat {tOy}\)là hai góc kề nhau.

b) Có \(\widehat {xOt} = 12{0^o},\widehat {tOy} = 6{0^o}\)

Suy ra \(\widehat {xOt} + \widehat {tOy} = {120^o} + {60^o} = {180^o}\)

Khi đó \(\widehat {xOt},\widehat {tOy}\) là hai góc bù nhau.

c) Vì \(\widehat {xOt},\widehat {tOy}\) là hai góc vừa kề nhau vừa bù nhau nên \(\widehat {xOt},\widehat {tOy}\) là hai góc kề bù.

Ví dụ 2. Hai đường thẳng xz và yt cắt nhau tại A như hình vẽ bên, hãy xác định các cặp góc đối đỉnh có trong hình vẽ.

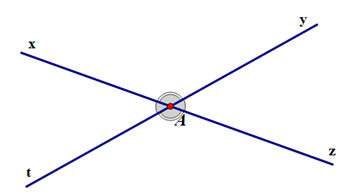
Hướng dẫn giải:

- Vì hai đường thẳng xz và yt cắt nhau tại A nên ta có: Hai tia Ax và Az đối nhau; hai tia Ay và At đối nhau.

- Xét hai góc \(\widehat {xAt}\) và \(\widehat {yAz}\) có:

+ Chung đỉnh A.

+ Tia Ax là tia đối của tia Az; tia At là tia đối của tia Ay.

Do đó \(\widehat {xAt}\) và \(\widehat {yAz}\) là hai góc đối đỉnh.

- Xét hai góc \(\widehat {xAy}\) và \(\widehat {tAz}\) có:

+ Chung đỉnh A.

+ Tia Ax là tia đối của tia Az; tia Ay là tia đối của tia At.

Do đó \(\widehat {xAy}\) và \(\widehat {tAz}\) là hai góc đối đỉnh.

Vậy ta có hai cặp góc đối đỉnh là: \(\widehat {xAt}\) và \(\widehat {yAz}\); \(\widehat {xAy}\) và \(\widehat {tAz}\).