Lý thuyết Vận dụng định nghĩa, tính chất của tam giác cân để chứng minh tính chất khác

a) Định nghĩa

Tam giác cân là tam giác có hai cạnh bên bằng nhau.

b) Tính chất

+ Nếu ∆ABC cân tại A thì \[\widehat {ABC} = \widehat {ACB}\];

+ Xét ∆ABC, nếu \[\widehat {ABC} = \widehat {ACB}\] thì ∆ABC cân tại A.

Ta sẽ sử dụng định nghĩa, tính chất của tam giác cân để suy ra hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau. Từ đó ta sẽ có thêm dữ kiện để chứng minh sự bằng nhau của hai tam giác, hai đoạn thẳng, hai góc.

Ví dụ 1. Cho ∆ABC cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = EC. Gọi M, N là hình chiếu của D, E trên AB, AC. Chứng minh rằng ∆AMD = ∆ANE.

Hướng dẫn giải:

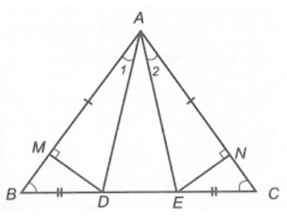
Xét ∆ADB và ∆AEC, có:

BD = EC (giả thiết).

\[\widehat {ABD} = \widehat {ACE}\] (∆ABC cân tại A).

AB = AC (∆ABC cân tại A).

Do đó ∆ADB = ∆AEC (cạnh – góc – cạnh).

Suy ra \[\widehat {{A_1}} = \widehat {{A_2}}\] và AD = AE (cặp góc và cặp cạnh tương ứng).

Xét ∆AMD và ∆ANE, có:

\[\widehat {AMD} = \widehat {ANE} = 90^\circ \].

\[\widehat {{A_1}} = \widehat {{A_2}}\] (chứng minh trên).

AD = AE (chứng minh trên).

Do đó ∆AMD = ∆ANE (cạnh huyền – góc nhọn).

Ví dụ 2. Cho ∆ABC cân tại A có M, N lần lượt là trung điểm của AC, AB. Từ M, N, kẻ đường thẳng vuông góc với AC và AB, hai đường thẳng này cắt BC lần lượt tại D và E. Chứng minh rằng:

a) ∆BNE = ∆CMD.

b) BD = CE.

Hướng dẫn giải:

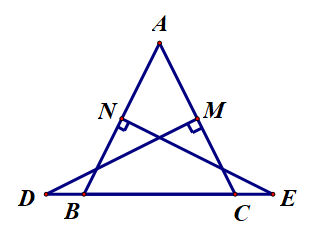
a) Vì N là trung điểm AB nên AB = 2BN (1).

Vì M là trung điểm AC nên AC = 2CM (2).

Vì ∆ABC cân tại A nên AB = AC (3).

Từ (1), (2), (3), ta suy ra BN = CM.

Xét ∆BNE và ∆CMD, có:

\[\widehat {BNE} = \widehat {CMD} = 90^\circ \].

BN = CM (chứng minh trên)

\[\widehat {NBE} = \widehat {MCD}\] (∆ABC cân tại A).

Do đó ∆BNE = ∆CMD (góc – cạnh – góc).

b) Ta có ∆BNE = ∆CMD (chứng minh trên).

Suy ra BE = CD.

Vì B, D, C thẳng hàng và B nằm giữa C, D nên ta có CD = BC + BD.

Vì B, E, C thẳng hàng và C nằm giữa B, E nên ta có BE = BC + CE.

Từ BE = CD, ta suy ra BC + CE = BC + BD.

Do đó CE = BD.

Vậy CE = BD.