Lý thuyết Tính số đo các góc dựa vào tính chất góc ở vị trí đặc biệt, định nghĩa tia phân giác

a) Tính số đo các góc dựa vào tính chất góc ở vị trí đặc biệt

Để tính số đo các góc ở vị trí đặc biệt, ta sử dụng các tính chất sau:

* Tính chất hai góc bù nhau:

Nếu \(\widehat {aOb}\) và \(\widehat {cOd}\) là hai góc bù nhau thì \(\widehat {aOb}\) + \(\widehat {cOd}\) = 180°.

* Tính chất hai góc kề bù:

Nếu \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = {180^o}\).

* Tính chất hai góc đối đỉnh:

Nếu \(\widehat {aOb}\) và \(\widehat {cOd}\) là hai góc đối đỉnh thì \(\widehat {aOb}\) = \(\widehat {cOd}\).

* Tính chất tia phân giác của một góc:

Nếu Oc là tia phân giác của \(\widehat {aOb}\) thì \(\widehat {aOc} = \widehat {cOb} = \frac{{\widehat {aOb}}}{2}\).

b) Định nghĩa tia phân giác

Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

Ví dụ 1. Cho hai đường thẳng xt và yz cắt nhau tại A sao cho \(\widehat {xAy} = 5{5^o}\). Hãy tính số đo các góc sau:

a) \(\widehat {xAz}\);

b) \(\widehat {zAt}\);

c) \(\widehat {yAt}\).

Hướng dẫn giải:

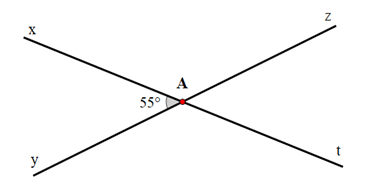
a) Vì \(\widehat {xAy}\) và \(\widehat {xAz}\) là hai góc kề bù nên \(\widehat {yAx} + \widehat {xAz} = \widehat {yAz} = 18{0^o}\).

Suy ra \[\widehat {xAz} = {180^o} - \widehat {xAy} = {180^o} - {55^o} = {125^o}\];

b) Vì \(\widehat {xAy}\) và \(\widehat {zAt}\) là hai góc đối đỉnh nên \(\widehat {zAt} = \widehat {xAy} = 5{5^o}\);

c) Vì \(\widehat {xAz}\) và \(\widehat {yAt}\) là hai góc đối đỉnh nên \(\widehat {yAt} = \widehat {xAz} = 12{5^o}\).

Ví dụ 2. Cho \(\widehat {xOy} = {150^o}\) và Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {xOz}\) và \(\widehat {zOy}\).

Hướng dẫn giải:

Vì Oz là tia phân giác của \(\widehat {xOy}\) nên:

\(\widehat {xOz}\) = \(\widehat {zOy}\) = \(\frac{{\widehat {xOy}}}{2} = \frac{{{{150}^o}}}{2} = {75^o}\).