Lý thuyết Tìm và chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc Từ đó chứng minh các cạnh bằng nhau và các góc bằng nhau, tính độ dài cạnh và số đo góc
- Để chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc ta làm theo các bước:
+ Xét hai tam giác;
+ Kiểm tra một cặp cạnh bằng nhau và hai cặp góc kề cạnh đó bằng nhau;
+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).
- Sử dụng trường hợp bằng nhau góc – cạnh – góc để chứng minh các cạnh, các góc bằng nhau, tính số đo góc ta làm theo các bước:
+ Xác định hai tam giác có các cạnh, các góc cần chứng minh bằng nhau hoặc cạnh cần tính độ dài hay góc cần tính số đo;
+ Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc;
+ Suy ra hai cạnh tương ứng bằng nhau, hai góc tương ứng bằng nhau hoặc độ dài cạnh hay số đo góc cần tính.
Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.
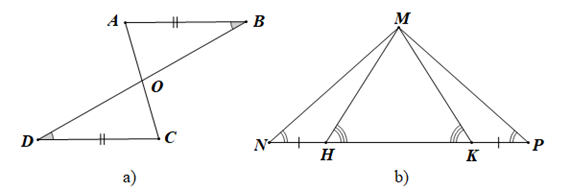
Ví dụ 1. Hãy kể tên các cặp tam giác bằng nhau theo trường hợp góc – cạnh – góc trong mỗi hình vẽ dưới đây:
Hướng dẫn giải
+ Xét hình a)
Vì \(\widehat B = \widehat D\) mà hai góc này ở vị trí so le trong
Nên AB // CD (dấu hiệu nhận biết)
Suy ra \(\widehat A = \widehat C\)
Xét tam giác ABO và CDO có:
\(\widehat A = \widehat C\) (chứng minh trên),
AB = CD (giả thiết),
\(\widehat B = \widehat D\) (giả thiết)
Do đó DABO = DCDO (g.c.g)
+ Xét hình b)
Ta có: NK = NH + HK và PH = PK + KH
Mà NH = PK do đó NK = PH
Xét tam giác MNK và tam giác MPH có:
\(\widehat N = \widehat P\) (giả thiết),
NK = PH (chứng minh trên),
\(\widehat {MKN} = \widehat {MHP}\) (giả thiết)
Do đó DMNK = DMPH (g.c.g)
Ta có: \(\widehat {MHN} + \widehat {MHP} = 180^\circ \) (tính chất hai góc kề bù)
\(\widehat {MKP} + \widehat {MKN} = 180^\circ \) (tính chất hai góc kề bù)
Mà \(\widehat {MKN} = \widehat {MHP}\) (giả thiết) do đó \(\widehat {MHN} = \widehat {MKP}\)
Xét tam giác MHN và tam giác MKP có:
\(\widehat N = \widehat P\) (giả thiết),
NH = PK (giả thiết),
\(\widehat {MHN} = \widehat {MKP}\) (chứng minh trên)
Do đó DMHN = DMKP (g.c.g).
Ví dụ 2. Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC tại E. Đường thẳng qua E và song song với AB cắt BC tại G. Chứng minh:
a) AD = EG;
b) DDAE = DGEC;
c) G là trung điểm của BC.
Hướng dẫn giải
|
GT |
DABC, D là trung điểm của AB, DE // BC (E ∈ AC), EG // AB (G ∈ BC), |
|
KL |
a) AD = EG; b) DDAE = DGEC; c) G là trung điểm của BC. |
Chứng minh (hình vẽ dưới đây):
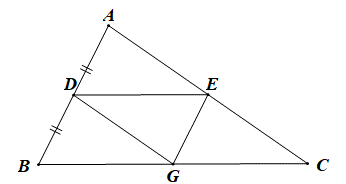
a) Vì DE // BC (giả thiết) nên \(\widehat {EDG} = \widehat {BGD}\) (hai góc so le trong)
Vì EG // AB (giả thiết) nên \(\widehat {EGD} = \widehat {BDG}\) (hai góc so le trong)
Xét DEGD và DBDG có:
\(\widehat {EDG} = \widehat {BGD}\) (chứng minh trên),
DG là cạnh chung,
\(\widehat {EGD} = \widehat {BDG}\)(chứng minh trên)
Do đó DEGD = DBDG (g.c.g)
Suy ra EG = BD (hai cạnh tương ứng)
Mà AD = BD (do D là trung điểm của AB)
Do đó AD = EG.
b) Vì DE // BC (giả thiết) nên \(\widehat {ADE} = \widehat {DBG}\) (hai góc đồng vị)
Vì EG // AB (giả thiết) nên \(\widehat {DAE} = \widehat {GEC}\) và \(\widehat {DBG} = \widehat {EGC}\) (các cặp góc đồng vị)
Do đó \(\widehat {ADE} = \widehat {DBG} = \widehat {EGC}\)
Xét DADE và DEGC có:
\(\widehat {DAE} = \widehat {GEC}\) (chứng minh trên),
AD = EG (chứng minh câu a),
\(\widehat {ADE} = \widehat {EGC}\)(chứng minh trên),
Do đó DADE = DEGC (g.c.g)
Vậy DADE = DEGC.
c) Từ DADE = DEGC (chứng minh câu b) nên DE = GC (hai cạnh tương ứng)
Mà DEGD = DBDG (chứng minh câu a) nên DE = GB (hai cạnh tương ứng)
Do đó GC = GB (= DE)
Vậy G là trung điểm của BC.