Lý thuyết Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh từ đó chứng minh tính chất khác

- Để chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh ta làm theo các bước:

+ Xét hai tam giác;

+ Kiểm tra ba cặp cạnh tương ứng bằng nhau;

+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

- Sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh để chứng minh các góc bằng nhau, tính số đo góc ta làm theo các bước:

+ Xác định hai tam giác có các góc cần chứng minh bằng nhau hoặc cần tính số đo;

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh;

+ Suy ra hai góc tương ứng bằng nhau hoặc số đo góc cần tính.

Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.

2. Ví dụ minh họa:

Ví dụ 1. Trong mỗi hình vẽ dưới đây có những tam giác nào bằng nhau theo trường hợp cạnh – cạnh – cạnh?

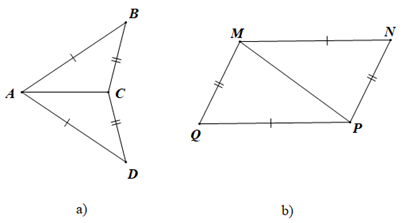
Hướng dẫn giải

a)

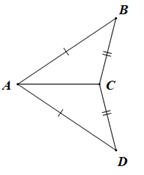
Xét tam giác ABC và tam giác ACD có:

AB = AD, BC = DC, AC là cạnh chung

Suy ra DABC = DADC (c.c.c)

Vậy DABC = DADC.

b)

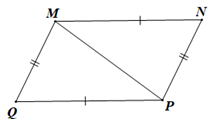
Xét tam giác MNP và tam giác MPQ có:

MN = PQ, NP = QM, MP là cạnh chung

Suy ra DMNP = DPQM (c.c.c)

Vậy DMNP = DPQM.

Ví dụ 2. Cho \(\widehat {xOy},\) trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ các cung tròn tâm C và D có cùng bán kính sao cho chúng cắt nhau ở điểm E nằm trong góc xOy. Chứng minh OE là tia phân giác của góc xOy.

Hướng dẫn giải

Chứng mính (Hình vẽ dưới đây):

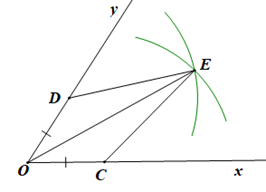
Vì các cung tròn tâm C và tâm D có cùng bán kính cắt nhau ở điểm E nằm trong góc xOy (giả thiết) nên ta có CE = DE

Xét tam giác OCE và tam giác ODE có:

OC = OD (giả thiết),

CE = DE (chứng minh trên),

OE là cạnh chung

Suy ra DOCE = DODE (c.c.c)

Do đó \(\widehat {COE} = \widehat {DOE}\) (hai góc tương ứng)

Nên tia OE là tia phân giác của góc xOy.

Vậy OE là tia phân giác của góc xOy.