Lý thuyết Chứng minh hai đường thẳng song song dựa vào dấu hiệu nhận biết
Để chứng minh hai đường thẳng song song với nhau, ta sử dụng một trong các dấu hiệu nhận biết sau:
+ Hai đường thẳng song song là hai đường thẳng không có điểm chung.
+ Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng song song với nhau.
+ Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng song song với nhau.
+ Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song với nhau.
+ Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ 1. Chứng minh đường thẳng ab song song với cd trong các trường hợp sau:
a)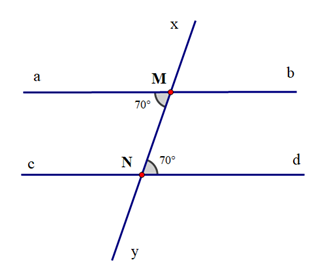 
b)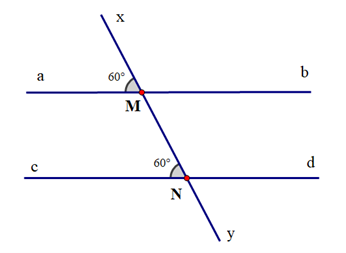 
c)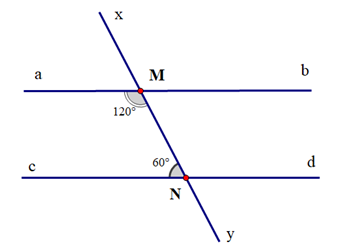 
d)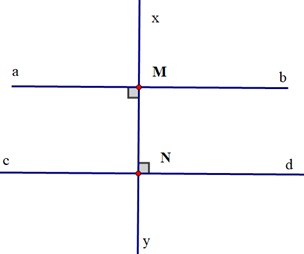 
Hướng dẫn giải:
a) Ta có \(\widehat {aMN} = \widehat {MNd} = {70^o}\).
Mà \(\widehat {aMN}\) và \(\widehat {MNd}\) là hai góc ở vị trí so le trong.
Do đó ab song song với cd.
b) Ta có \(\widehat {xMa} = \widehat {MNc} = {60^o}\).
Mà \(\widehat {xMa}\) và \(\widehat {MNc}\) là hai góc ở vị trí đồng vị.
Do đó ab song song với cd.
c) Ta có \(\widehat {aMN} + \widehat {MNc} = {120^o} + {60^o} = {180^o}\).
Suy ra \(\widehat {aMN}\) và \(\widehat {MNc}\) là hai góc bù nhau.
Mà \(\widehat {aMN}\) và \(\widehat {MNc}\) là hai góc ở vị trí trong cùng phía.
Suy ra ab song song với cd.
d) Vì ab và cd là hai đường thẳng phân biệt cùng vuông góc với đường thẳng xy nên chúng song song với nhau.
Ví dụ 2. Cho hình vẽ:
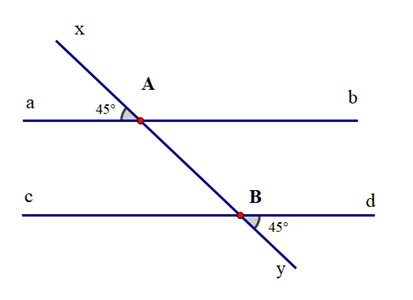
Biết \(\widehat {xAa} = \widehat {yBd} = {45^o}\). Hai đường thẳng ab và cd có song song với nhau không? Vì sao?
Hướng dẫn giải:
Do \(\widehat {xAa}\) và \(\widehat {bAB}\) là hai góc đối đỉnh nên \(\widehat {xAa}\)= \(\widehat {bAB}\) = 45°.
Suy ra \(\widehat {bAB}\) = \(\widehat {dBy}\) (cùng bằng 45°).
Mà \(\widehat {bAB}\) và \(\widehat {dBy}\) là hai góc ở vị trí đồng vị.
Suy ra ab song song với cd.