Lý thuyết Tính số đo các góc dựa vào tính chất hai đường thẳng song song

Để tính số đo các góc dựa vào tính chất của hai đường thẳng song song thì ta cần nắm được tính chất sau:

Nếu một đường thẳng cắt hai đường thẳng song song thì:

+ Hai góc so le trong bằng nhau.

+ Hai góc đồng vị bằng nhau.

Ta có thể kết hợp với một số tính chất khác như: hai góc kề bù, hai góc đối đỉnh, tia phân giác của một góc,…để tính số đo góc cần tìm.

Ví dụ 1. Cho hình vẽ, biết xx’ // yy’ và \(\widehat {xAB} = {60^o}\). Tính số đo các góc \(\widehat {ABy'}\), \(\widehat {ABy}\), \(\widehat {yBz'}.\)

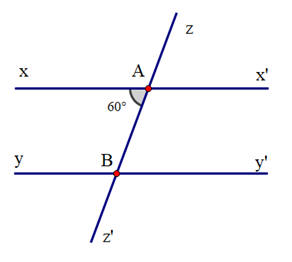
Hướng dẫn giải:

+ Ta có xx’ // yy’, suy ra \(\widehat {xAB} = \widehat {ABy'}\) (hai góc so le trong)

Suy ra \(\widehat {ABy'} = {60^o}\).

+ Ta có xx’ // yy’, suy ra \(\widehat {xAB} = \widehat {yBz'}\) (hai góc đồng vị)

Suy ra \(\widehat {yBz'} = {60^o}\).

+ Ta có \(\widehat {ABy}\) và \(\widehat {ABy'}\) là hai góc kề bù nên \(\widehat {ABy}\) + \(\widehat {ABy'}\) = 180°

Suy ra \(\widehat {ABy} = {180^o} - \widehat {ABy'} = {180^o} - {60^o} = {120^o}\).

Ví dụ 2. Cho hình vẽ sau:

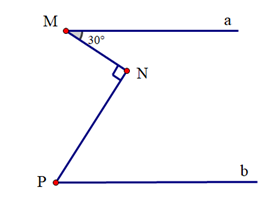
Biết Ma // Pb; MN ⊥ NP; \(\widehat {NMa}\) = 30°. Tính \(\widehat {NPb}\)

Hướng dẫn giải:

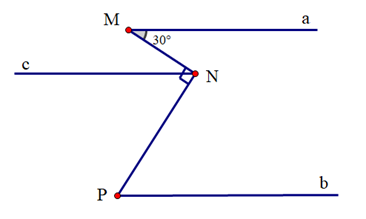
Kẻ Nc // Ma

Suy ra \(\widehat {MNc} = \widehat {NMa} = 30^\circ \) (hai góc so le trong)

Ta có \(\widehat {MNP} = \widehat {MNc} + \widehat {cNP}\) (hai góc kề nhau)

Suy ra \(\widehat {cNP} = \widehat {MNP} - \widehat {MNc}\)

Mà \(\widehat {MNP} = 90^\circ \) (do MN ⊥ NP)

Suy ra \(\widehat {cNP} = 90^\circ  - 30^\circ  = 60^\circ \)

Ta có Nc // Ma, mà Ma // Pb

Suy ra Nc // Pb (vì cùng song song với Ma)

Suy ra \(\widehat {NPb} = \widehat {cNP} = 60^\circ \) (hai góc so le trong)

Vậy \(\widehat {NPb} = 60^\circ \)