Lý thuyết Xác định các cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía trên hình vẽ cho trước

Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại hai điểm A và B tạo thành 4 góc đỉnh A và 4 góc đỉnh B được đánh số như trên hình vẽ:

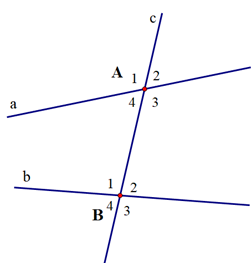
Ta sắp xếp các góc thành từng cặp như sau:

a) Hai cặp góc so le trong

\({\widehat A_4}\) và \({\widehat B_2}\); \({\widehat A_3}\) và \({\widehat B_1}\)

b) Bốn cặp góc đồng vị

\({\widehat A_1}\) và \({\widehat B_1}\); \({\widehat A_2}\) và \({\widehat B_2}\); \({\widehat A_3}\) và \({\widehat B_3}\); \({\widehat A_4}\) và \({\widehat B_4}\)

c) Hai cặp góc trong cùng phía

\({\widehat A_4}\) và \({\widehat B_1}\); \({\widehat A_3}\) và \({\widehat B_2}\)

Ví dụ 1. Cho đường thẳng xy cắt hai đường thẳng ab và cd lần lượt tại hai điểm M và N như hình vẽ.  

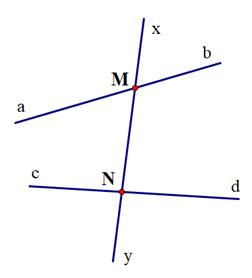
Hãy xác định:

a) Hai cặp góc so le trong;

b) Bốn cặp góc đồng vị;

c) Hai cặp góc trong cùng phía.

Hướng dẫn giải:

a) Hai cặp góc so le trong: \(\widehat {aMN}\) và \(\widehat {MNd}\); \(\widehat {bMN}\) và \(\widehat {MNc}\).

b) Bốn cặp góc đồng vị: \(\widehat {xMa}\) và \(\widehat {MNc}\); \(\widehat {xMb}\) và \(\widehat {MNd}\); \(\widehat {aMN}\) và \(\widehat {cNy}\); \(\widehat {bMN}\) và \(\widehat {dNy}\).

c) Hai cặp góc trong cùng phía: \(\widehat {aMN}\) và \(\widehat {MNc}\); \(\widehat {bMN}\) và \(\widehat {MNd}\).

Ví dụ 2. Cho hình vẽ sau:

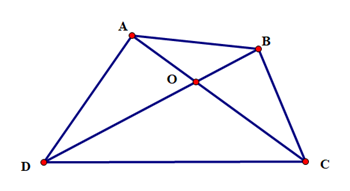
Điền vào chỗ trống (…) trong các câu sau:

a) \(\widehat {BAC}\) và \(\widehat {ACD}\) là một cặp góc …;

b) \(\widehat {BAO}\) và \(\widehat {BOC}\) là một cặp góc …;

c) \(\widehat {DAC}\) và \(\widehat {ACB}\) là một cặp góc …;

d) \(\widehat {AOD}\) và \(\widehat {OCD}\) là một cặp góc ….

Hướng dẫn giải:

a) \(\widehat {BAC}\) và \(\widehat {ACD}\) là một cặp góc so le trong;

b) \(\widehat {BAO}\) và \(\widehat {BOC}\) là một cặp góc đồng vị;

c) \(\widehat {DAC}\) và \(\widehat {ACB}\) là một cặp góc so le trong;

d) \(\widehat {AOD}\) và \(\widehat {OCD}\) là một cặp góc đồng vị.