Lý thuyết Vận dụng tiên đề Euclid về hai đường thẳng song song và chứng minh ba điểm thẳng hàng

Tiên đề Euclid:

“Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.”

Nếu A ∈ a, A ∉ b thì chỉ có một đường thẳng a thoả mãn a // b.

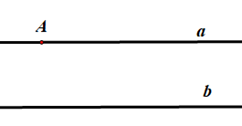
Do đó ta có thể sử dụng tiên đề Euclid để chứng minh ba điểm thẳng hàng như sau:

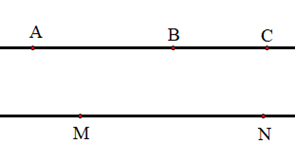
Giả sử có: AB // MN, AC // MN (hình vẽ).

Mà hai đường thẳng AB và AC đều đi qua A.

Theo tiên đề Euclid: chỉ có một đường thẳng đi qua A và song song với MN.

Nên hai đường thẳng AB và AC trùng nhau.

Hay ba điểm A, B, C thẳng hàng.

Ví dụ 1. Cho AB // CD. Trên tia đối của tia BA lấy điểm E. Chứng minh BE // CD.

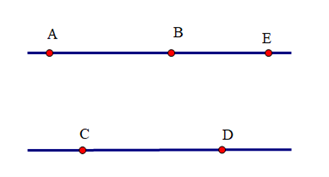
Hướng dẫn giải:

Ta có hai đường thẳng AB và CD song song với nhau.

Mà E nằm trên tia đối của tia BA.

Theo tiên đề Euclid ta có: Qua B chỉ kẻ được duy nhất một đường thẳng song song với CD.

Suy ra BE song song với CD.

Ví dụ 2. Cho MN // PQ; NO // PQ. Chứng minh ba điểm M, N, O thẳng hàng.

Hướng dẫn giải:

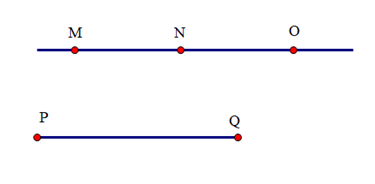
Theo tiên đề Euclid: chỉ có một đường thẳng đi qua N và song song với PQ.

Mà hai đường thẳng MN và NO đều đi qua N và song song với PQ.

Suy ra hai đường thẳng MN và NO trùng nhau.

Do đó ba điểm M, N, O thẳng hàng.

Vậy ba điểm M, N, O thẳng hàng.